Basic Trigonometric Ratios and their Names
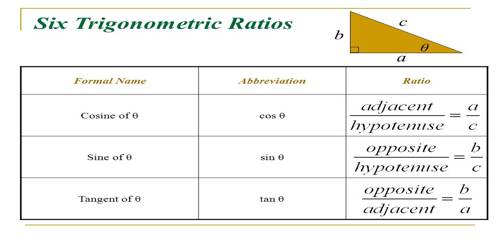
“Trigon” is Greek for the triangle, and “metric” is Greek for measurement. The trigonometric ratios are special measurements of a right triangle (a triangle with one angle measuring 90°). Remember that the two sides of a right triangle which form the right angle are called the legs, and the third side (opposite the right angle) is called the hypotenuse.
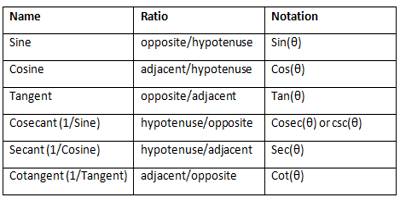
- The sine of the angle is the ratio of the length of the side opposite the angle divided by the length of the hypotenuse. It is the trigonometric function that is equal to the ratio of the side opposite a given angle (in a right-angled triangle) to the hypotenuse.
- The cosine of the angle is the ratio of the length of the side adjacent to the angle divided by the length of the hypotenuse. It is the trigonometric function that is equal to the ratio of the side adjacent to an acute angle (in a right-angled triangle) to the hypotenuse.
- The tangent of the angle is the ratio of the length of the side opposite the angle divided by the length of side adjacent to the angle.
Let us consider the right-angled triangle ABO as shown in the adjacent figure. Now, with respect to the acute angle ∠AOB = θ, the adjacent side OA becomes the hypotenuse and the other (adjacent) side OB becomes the base. So, in this case, AB becomes the perpendicular.
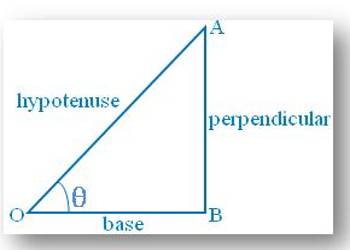
Then AB/OA = perpendicular/hypotenuse = Sine of θ or briefly sin θ
OB/OA = base/hypotenuse = Cosine of θ or briefly cos θ
AB/OB = perpendicular/base = Tangent of θ or briefly tan θ
OA/AB = hypotenuse/perpendicular = Cosecant of θ or briefly cosec θ
OA/OB = hypotenuse/base = Secant of θ or briefly sec θ
OB/AB = base/perpendicular = Cotangent of θ or briefly cot θ
N.B. The side opposite to the angle under reference is to be taken as perpendicular and the side adjacent to it except the hypotenuse as the base.
Like all other ratios, these ratios are also pure numbers and have no units.
In the beginning of this topic, we have become acquainted with the above property. Let us discuss here ore categorically.
Note:
- The side opposite to the angle under reference is to be taken as perpendicular and the side adjacent to it except the hypotenuse as the base.
- Like all other ratios, these ratios are also pure numbers and have no units.
- In right-angled triangle OBA, ∠BOA lies between 0° to 90° i.e. ∠BOA is acute angle i.e. θ is the acute angle and also six trigonometrical ratios are positive.
- Each trigonometrical ratio is a real number.
Information Source: