Triangle is a plane figure with three straight sides and three angles. The three angles always add to 180°. The vertex is a corner of the triangle. Every triangle has three vertices. The interior angles of a triangle always add up to 180°. The exterior angles of a triangle always add up to 360°.
Classification of Triangles on the Basis of their Angles
Acute-angled triangle: A triangle which contains acute angles as interior angles is called an acute-angled triangle. If all the three angles of a triangle are acute angles (i.e., each measure less than 90°), it is called an acute-angled triangle.
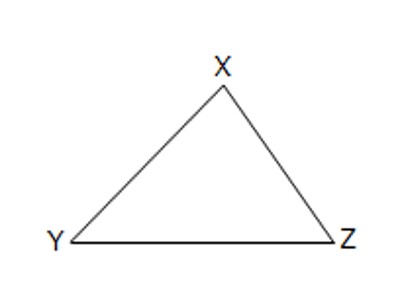
Fig: Acute-angled Triangle
Here, ∠XYZ, ∠YZX, and ∠ZXY are all acute angles.
Right-angled triangle: If one of the angles of a triangle is a right angle (i.e., measures 90°), it is called a right-angled triangle. A triangle cannot have more than 1 right angle. If the lengths of all three sides of a right triangle are integers, the triangle is said to be a Pythagorean triangle and its side lengths are collectively known as a Pythagorean triple.
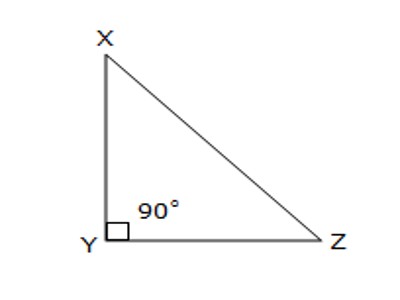
Fig: Right-angled Triangle
Here, <XYZ = 90°.
Therefore, ∆ XYZ is a right-angled triangle.
Obtuse-angled triangle: If all the three angles of a triangle is an obtuse angle (i.e., measures more than 90°), it is called an obtuse-angled triangle. An obtuse triangle is one with one obtuse angle (greater than 90°) and two acute angles. A triangle cannot have more than one obtuse angle. Since a triangle’s angles must sum to 180°, no triangle can have more than one obtuse angle.
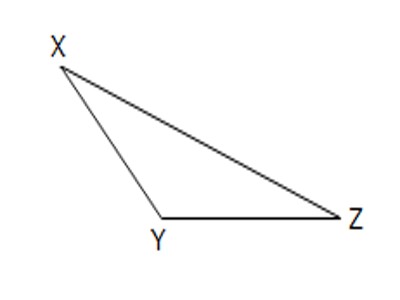
Fig: Obtuse-angled Triangle
Here, ∠XYZ > 90°.
Therefore, ∆ XYZ is an obtuse-angled triangle.
Information Source: