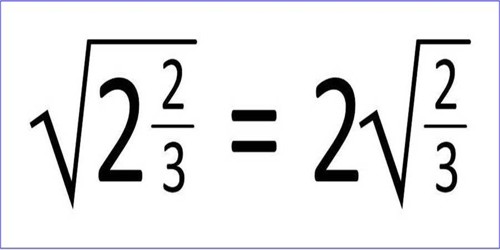Comparison of Surds

Definitions of surds: A root of a positive real quantity is called a surd if its value cannot be exactly determined. It is a number that can’t be simplified to remove a square root (or cube root etc). For example, each of the quantities √3, ∛7, ∜19, (16)^2/5 etc. is a surd.

More Examples:

√2 (square root of 2) can’t be simplified further so it is a surd
√4 (square root of 4) CAN be simplified to 2, so it is NOT a surd

Comparison of Surds

In the comparison of surds, we will discuss the comparison of equiradial surds and comparison of non-equiradical surds.

Comparison of equiradical surds:

In case of equiradical surds (i.e., surds of the same order) ⁿ√a and ⁿ√b, we have ⁿ√a > ⁿ√b when x > y.

For example,

(i) √5 > √3, since 5 > 3

(ii) ∛21 < ∛28, since 21 < 28.

(iii) ∜10 > ∜6, since 10 > 6.

Comparison of non–equiradical surds:

In case of comparison between two or more non-equiradical surds (i.e., surds of different orders) we express them to surds of the same order (i.e., equiradical surds). Thus, to compare between ∛7 and ∜5 we express them to surds of the same order as follows:

Clearly, the orders of the given surds are 3 and 4 respectively and LCM Of 3 and 4 is 12.

Therefore, ∛7 = 7^1/3 = 7^4/12 = ¹²√7⁴ = ¹²√2401 and

∜5 = 5^1/4 = 5^3/12 = ¹²√5³ = ¹²√125

Clearly, we see that 2401 > 125

Therefore, ∛7 > ∜5.

Example of comparison of surds:

Convert each of the following surds into equiradical surds of the lowest order and then arrange them in ascending order.

∛2, ∜3 and ¹²√4

Solution:

∛2, ∜3 and ¹²√4

We see that the orders of the given surds are 3, 4 and 12 respectively.

Now we need to find the lowest common multiple of 3, 4 and 12.