Locus is a curve or other figure formed by all the points satisfying a particular equation of the relation between coordinates, or by a point, line, or surface moving according to mathematically defined conditions.
It is the set of all points (usually forming a curve or surface) satisfying some condition. For example, the locus of points in the plane equidistant from a given point is a circle, and the set of points in three-space equidistant from a given point is a sphere. Example: A Circle is “the locus of points on a plane that are a certain distance from a central point”.
Consider a point that is moving in a plane. If we join each of the positions through which the moving point passes, we will get the path followed by the point. If the movement of the point is random, its path will be irregular, and we shall not be able to predict, for example, how its path will look when the point stops. Therefore, the path of a randomly moving point cannot be determined. On the other hand, if the point’s movement obeys a given set of rules, the resulting path will be predictable and can be a circle, a straight line, an ellipse, and so on.
The word locus describes the position of points which obey a certain rule
Three important loci are:
- The circle – the locus of points which are equidistant from a fixed point, the centre.
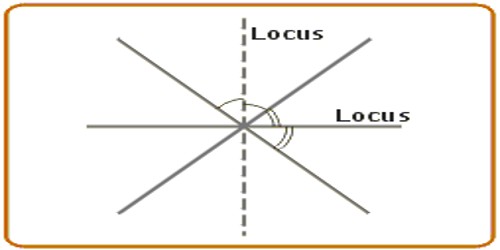
- The perpendicular bisector – the locus of points which are equidistant from two fixed points A and B.
- The angle bisector – the locus of points which are equidistant from two fixed lines.
So, you can look upon a circle, a straight line, and so on, as a set of points positioned according to a given rule or rules.
Definition of locus: A path consisting of a set of points whose location is governed by some definite rule of rules is called locus. Locus in Latin means “position” or “location”.
Examples:
Let a point P move in such a way that it is always at a constant distance, r, from ma fixed point O.
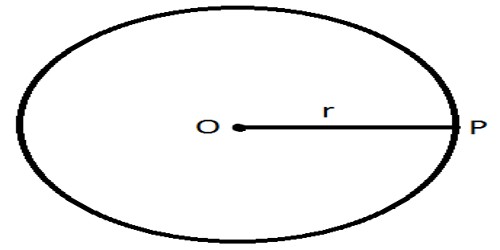
The locus of a point P is a circle which has its center at O and has a radius equal to r units.
Strategy for Solving Locus Problems:
- Draw a diagram using the given information.
- Read carefully to determine what conditions need to be satisfied.
- Start by finding ONE point that satisfies the needed conditions and plot it on your diagram. Then find several additional points that satisfy the conditions and plot them as well. Continue plotting points until you can see the pattern, or path, that is developing.
- Draw a dashed line, or circle, through the plotted points to show the locus.
- If you are asked to describe your locus in writing, be very specific so you will give a clear description of your work.
- If TWO, or more, conditions exist in the problem (a compound locus), repeat steps 2 through 5 for the additional conditions on the same diagram. You will know you have a compound locus when you see the words “AND” or “AND ALSO” separating the conditions.
- For a compound locus, count the number of locations where the two loci intersect (where the dashed drawings cross). Clearly label these locations on the diagram, or describe them in words.
Information Source: