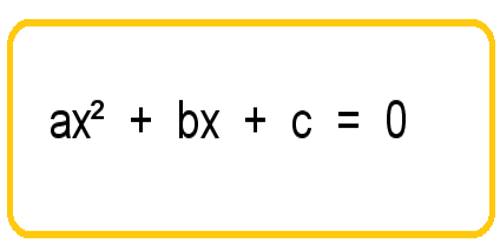Condition for Common Root of Quadratic Equations
A polynomial of the second degree is generally called a quadratic polynomial. In elementary algebra, the quadratic formula is the solution of the quadratic equation. There are other ways to solve the quadratic equation instead of using the quadratic formula, such as factoring, completing the square, or graphing. Using the quadratic formula is often the most convenient way.
If f(x) is a quadratic polynomial, then f(x) = 0 is called a quadratic equation.
An equation in one unknown quantity in the form ax2 + bx + c = 0 is called quadratic equation.
Condition for one common root:
Let the two quadratic equations are a1x2 + b1x + c1 = 0 and a2x2 + b2x + c2 = 0
Now we are going to find the condition that the above quadratic equations may have a common root.
Let α be the common root of the equations a1x2 + b1x + c1 = 0 and a2x2 + b2x + c2 = 0. Then,
a1α2 + b1α + c1 = 0
a2α2 + b2α + c2 = 0
Now, solving the equations a1α2 + b1α + c1 = 0, a2α2 + b2α + c2 = 0 by cross-multiplication, we get
α2/b1c2 – b2c1 = α/c1a2 – c2a1 = 1/a1b2 – a2b1
⇒ α = b1c2 – b2c1/c1a2 – c2a1, (From first two)
Or, α = c1a2 – c2a1/a1b2 – a2b1, (From 2nd and 3rd)
⇒ b1c2 – b2c1/c1a2 – c2a1 = c1a2 – c2a1/a1b2 – a2b1
⇒ (c1a2 – c2a1)2 = (b1c2 – b2c1)(a1b2 – a2b1), which is the required condition for one root to be common of two quadratic equations.
The common root is given by α = c1a2 – c2a1/a1b2 – a2b1 or, α = b1c2 – b2c1/c1a2 – c2a1
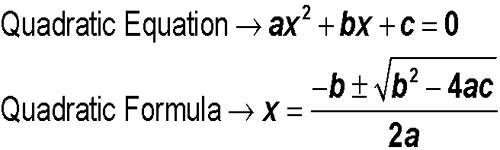
Note:
(i) We can find the common root by making the same coefficient of x2 of the given equations and then be subtracting the two equations.
(ii) We can find the other root or roots by using the relations between roots and coefficients of the given equations
Condition for both roots common:
Let α, β be the common roots of the quadratic equations a1x2 + b1x + c1 = 0 and a2x2 + b2x + c2 = 0. Then
α + β = -b1/a1, αβ = c1/a1 and α + β = -b2/a2, αβ = c2/a2
Therefore, -b/a1 = – b2/a2 and c1/a1 = c2/a2
⇒ a1/a2 = b1/b2 and a1/a2 = c1/c2
⇒ a1/a2 = b1/b2 = c1/c2
This is the required condition.
Information Source: