Conditions of Collinearity of Three Points
Collinearity implies the determinant (which represents the Area of the triangle with the aforementioned vertices) is zero.
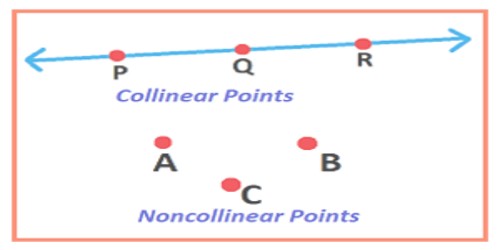
Collinear points: Three points A, B and C are said to be collinear if they lie on the same straight line. For any points that are collinear, just create the set of all parallel lines to your line (in one direction, out of the n-1 possibilities). Done, you have just created a plane that contains your line, which means your points lie on the same plane, which means the points are coplanar.
In 2 dimensions, then you just have the entire X-Y coordinate as your plane, any 2 or more collinear points are in the X-Y coordinate plane, so they are coplanar.
There points A, B and C will be collinear if AB + BC = AC as is clear from the adjoining figure.
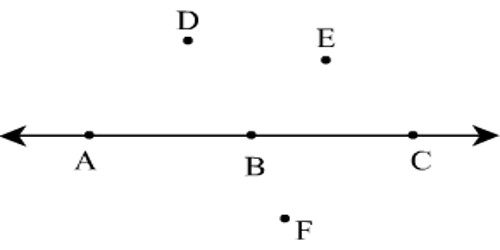
In general, three points A, B and C are collinear if the sum of the lengths of any two line segments among AB, BC and CA is equal to the length of the remaining line segment, that is, either AB + BC = AC or AC +CB = AB or BA + AC = BC.
In other words,
There points A, B and C are collinear if:
(i) AB + BC = AC i.e.,
Or, (ii) AB + AC = BC i.e. ,
Or, AC + BC = AB i.e.,
Information Source: