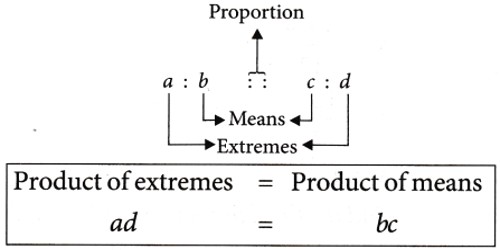
Three quantities are said to be in continued proportion if the ratio of the first term and second term be equal to the ratio of the second term and third term.
Continued proportion: Three numbers ‘a’, ‘b’ and ‘c’ are said to be continued proportion if a, b and c are in proportion.
Thus, if a, b and c are in continued-proportion, then
a,b,b,c are in proportion, that means; a : b : : b : c
⇒ Product of extremes = Product of means
⇒ a x c = b x b
⇒ a x c = b²
Continued-proportion is also known as mean proportional.
If ‘b’ is a mean proportional between a and c then b2 = ac.
Suppose, the three quantities x, y and z are said to be in continued proportion if x : y = y : z, i.e., x/y = y/z
Similarly, four quantities are said to be in continued proportion if the ratio of the first term and second term be equal to the ratio of the second term and third term be equal to the ratio of the third term and fourth term.
If w, x, y and z are four quantities such that w : x = x : y = y : z, i.e., w/x = x/y = y/z, they are said to be in continued proportion.
For example,
(i) The numbers 4, 6 and 9 are in continued proportion because
4/6 = 6/9
or, 62 = 4 × 9.
(ii) The numbers 2, 4 and 6 are not in continued proportion because
2/4 ≠ 4/6.
(iii) The numbers 2, 4, 8 and 16 are in continued proportion because
2/4 = 4/8 = 8/16.

Explanation
Suppose, if we have three qualities such that the ratio of first to second is equal to the ratio of second to third, we say that the three qualities are in continued proportion. The middle term is called the mean proportional between the first the third terms.
i.e. a, b and c are in continued proportion, if a : b = b : c
The second quantity is called the mean proportional between the first and the third
i.e. in a : b = b : c; b is the mean proportional between a and c.
The third quantity is called the third proportional to the first and the second
i.e. in a : b = b : c; c is the third proportional to a and b.
For example, let us consider the numbers 6, 12, 24.
Here the ratio of first quantity to the second = 6 : 12 = 1 : 2
And ratio of second quantity to the third = 12 : 24 = 1 : 2
We see that 6 : 12 = 12 : 24
Thus, 6, 12, 24 are in continued proportion.
The second quantity 12 is the mean proportional and third quantity 24 is the third proportional.
Information Source: