Differences between equation and inequation
Equations and inequation are both mathematical sentences formed by relating two expressions to each other. We have seen that equations are expressed by sign of equality and inequations are expressed by sign of inequality. We have also seen that a linear equation has one root and quadratic equation has two roots.
An equation is a statement that maintains the equal value of two mathematical expressions. If the statement is true for all variable values, it is called an identity. If it is only true for some variable values, it is called a conditional equation. An inequality, on the other hand, is a statement that uses the symbols > for greater than or < for lesser than to denote that one quantity is larger or smaller in value than another.
The equation, after simplification of terms, will show that the maximum power of the variable is equal to the variable is equal to number of roots. As the maximum power of x^2 + x – 2 = 0 is 2, so it has two roots namely 1 and -2. So, we see that the number of roots of an equation is definite but it is not true for inequation. To solve an equation, the value or values of the variable must be found that make both sides of the equation have the same value.
Solving Inequalities is very similar to solving Equations. The same general technique applies. That technique for solving equations is: Whatever you do to one side of the equation, you have to do to the other side to preserve the equality.
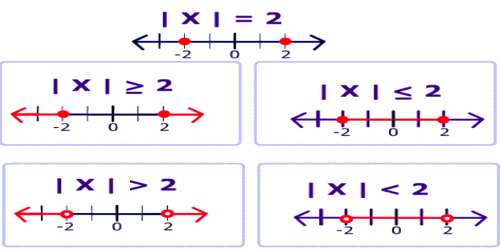
As for example, the inequation x < 5 is satisfied for any value of x less than 5, and the number of numbers less than 5 is infinite. Similarly, the inequation 2x – 3 ≥ 5 holds for an infinite number of values of x. Hence an inequation is satisfied by an infinite values of the unknown quantity. The set of values for which an inequation is satisfied is called the solution set of the inequation.
In an equation the two expressions are deemed equal which is shown by the symbol ‘=’. x = y; x is equal to y.
Where as in an inequality the two expressions are not necessarily equal which is shown by the symbols: >, <, ≤ or ≥.
x > y; x is greater than y
x ≥ y; x is greater than or equal to y
x < y; x is less than y
x ≤ y; x is less than or equal to y
Note:
An inequation with a given condition may have a finite number of solutions.
For example, for a positive integer, x ≤ 5 has the solution 1, 2, 3, 4, 5.
Hence we can denote the solution set of the inequation x ≤ 5 by {1, 2, 3, 4, 5}
Simple inequation: If an inequation contains an known quantity of power one only, it is called a simple inequation.
5x + 7 > 10, 6x – 8 ≥ 23, 5x + 3 ≤ 12 etc. Are simple inequations.
Information Source: