A mathematical statement is a differential equation; it is an equation that relates one or more functions and their derivatives. In science and engineering, as well as in many other fields of quantitative analysis, differential equations are very common because their rates of change are what can be directly observed and calculated for systems undergoing changes. In applications, the capacities for the most part speak to physical amounts, the subordinates speak to their paces of progress, and the differential condition characterizes a connection between the two. The basic role of the differential equation is the investigation of arrangements that fulfill the equations and the properties of the arrangements.
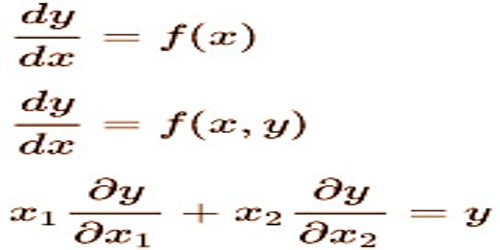
Differential Equation
In general, the solution of a differential equation is an equation which expresses the functional dependence of one variable on one or more others; it typically contains constant terms which are not present in the original differential equation. The analysis of differential equations consists primarily of studying their solutions (the set of functions that satisfy each equation), and the properties of their solutions. Mainly the study of differential equations consists of the study of their solutions (the set of functions that satisfy each equation), and of the properties of their solutions. Just the most straightforward differential equations are reasonable by express recipes; in any case, numerous properties of arrangements of a given differential equation might be resolved without processing them precisely. Another method of saying this is the arrangement of a differential equation delivers a capacity that can be utilized to anticipate the conduct of the first framework, in any event inside specific imperatives.
With the invention of calculus by Newton and Leibniz, differential equations first came into being. A differential equation is simply an equation containing one or more terms and derivatives of one variable ( i.e. dependent variable) relative to the other variable ( i.e. independent variable): dy/dx = f(x)
Here “x” is an independent variable and “y” is a dependent variable
For example, dy/dx = 5x
The motion of a body is defined in classical mechanics by its location and velocity as the time value varies. The laws of Newton allow these variables to be dynamically expressed as a differential equation of the unknown position of the body as a function of time (given the position, velocity, acceleration, and different forces acting on the body). In some cases, this differential equation (called an equation of motion) is also solved explicitly.
There are many large categories of differential equations, and these are further divided into several subcategories in turn. Ordinary differential equations and partial differential equations are the most important types. It includes derivatives that are either partial derivatives of common derivatives. The derivative represents a rate of change, and also the differential equation describes a relationship between the quantities that are continuously varying with relevancy the change in another quantity. At the point when the capacity engaged with the condition relies upon just a solitary variable, its subordinates are conventional subsidiaries and the differential equation is classed as a customary differential equation.
Differential equations can be divided into several types namely:
- Ordinary Differential Equations
- Partial Differential Equations
- Linear Differential Equations
- Non-linear differential equations
- Homogeneous Differential Equations
- Non-homogenous Differential Equations
These groups of differential equations, apart from defining the properties of the equation itself, can help inform the choice of approach to a solution. On the other hand, the differential equation is known as a partial differential equation if the function depends on many independent variables, such that its derivatives are partial derivatives. The following are examples of ordinary differential equations:
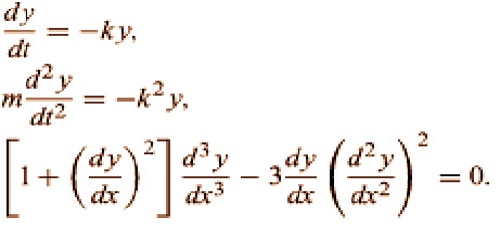
In these, y stands for the function, and the independent variable is either t or x. To stand for unique constants, the symbols k and m are used here. As in general, a closed-form expression cannot express the solutions of a differential equation, numerical methods are widely used to solve differential equations on a machine.
The order of the differential equation is the order of the very best order derivative present within the differential equation. Here a number of the examples for various orders of the differential equation are given.
dy/dx = 3x + 2 , The order of the equation is 1
(d2y/dx2)+ 2 (dy/dx)+y = 0. The order is 2
(dy/dt)+y = kt. The order is 1
Whatever the form maybe, if it has a derivative of the nth order but no derivative of an order greater than this, a differential equation is said to be of the nth order. The equation
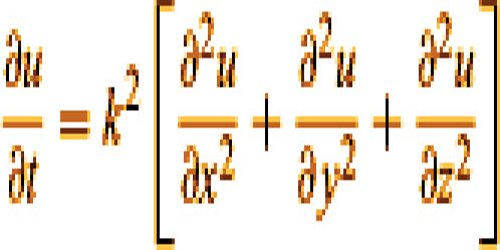
is an example of a partial differential equation of the second order. The theories of ordinary and partial differential equations vary markedly, and the two groups are viewed separately for this reason. Just as ordinary differential equations frequently model one-dimensional dynamical systems, multidimensional systems are often modeled by partial differential equations. Stochastic partial differential equations make partial differential equations generalized for random modeling.
The solution of differential equations does not imitate solving algebraic equations. Not only are their solutions often vague, but prominent areas of concern often include whether solutions are special or exist at all. The function and its derivatives are an ordinary differential equation. It contains just a single autonomous variable and at least one of its subordinates regarding the variable. The request for standard differential equations is characterized as the request for the most elevated subordinate that happens in the condition. By and large, a solitary differential equation of the nth request is profitably replaceable by an arrangement of n synchronous equations, every one of which is of the principal request, with the goal that procedures from straight variable based math can be applied.
In pure and applied mathematics, physics, and engineering, studying differential equations is a wide field. All those disciplines are concerned with the properties of various forms of differential equations. Thus, by indirect methods, most functions must be studied. And though there is no chance of manufacturing it for examination, its presence must be confirmed. In practice, numerical analysis methods, which require machines, are used to achieve useful approximate solutions.
Information Sources: