Distance Formula
The distance formula is used to determine the distance, d, between two points. As, we know the coordinates of two points in a plain fix the positions of the points in the plane and also the distance between them. The distance and the coordinates of the two points are related by an algebraic relation which can be deduced as shown below.
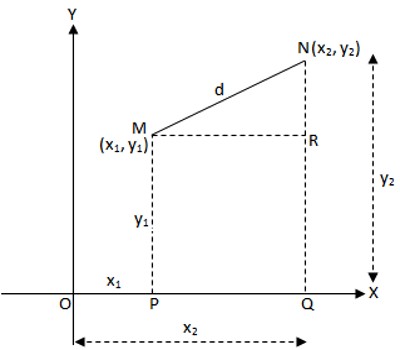
Let M (x1, y1) and N (x2, y2) are the two points in the plane. OX and OY being the rectangular axes of reference. Let MN = d. Draw MP ⊥ OX, NQ ⊥ OX and MR ⊥ NQ.
According to the definition of the co-ordinates,
OP = x1, MP = y1, OQ = x2, NQ = y2
From geometry, MR = PQ = OQ – OP = x2 – x1, and
NR = NQ – RQ = NQ – MP = y1 – y1.
In the right-angled triangle MRN,
MN2 = MR2 + NR2
or, d2 = (x2 – x1)2 + (y2 – y1)2
Therefore, d = √[(x2 – x1)2 +(y2 – y1)2]
The distance between two points (x1, y1) and (x2, y2) = √[(x2 – x1)2 +(y2 – y1)2]
= (difference of x − coordinates)2 + (difference of y − coordinates)2
The above formula is known as the distance formula.
Information Source: