Distributive, Identity and Inverse Axioms
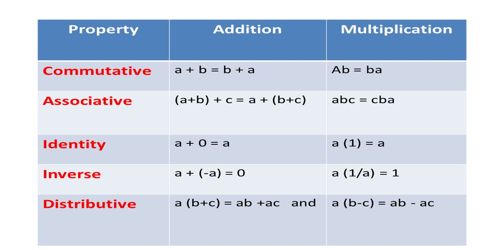
An Axiom is a mathematical statement that is assumed to be true. There are five basic axioms of algebra. Axioms are generally statements made about real numbers. Sometimes they are called algebraic postulates.
The Distributive Axioms are that x(y + z) = xy + xz and (y + z)x = yx + zx. This is the only property which combines both addition and multiplication.
These equations are true for all numbers x, y and z.
The Additive Identity Axiom states that a number plus zero equals that number. A number plus zero equals that number. (The number keeps its identity!)
x + 0 = x or 0 + x = x

The Multiplicative Identity Axiom states that a number multiplied by 1 is that number. A number times 1 equals that number. (The number keeps its identity!)
x*1 = x or 1*x = x
The Additive Inverse Axiom states that the sum of a number and the Additive Inverse of that number is zero. Every real number has a unique additive inverse. Zero is its own additive inverse. The sum of a number and the Additive Inverse of that number is zero. Every real number has a unique additive inverse. Zero is its own additive inverse.
x + (-x) = 0
The Multiplicative Inverse Axiom states that the product of a real number and its multiplicative inverse is 1. Every real number has a unique multiplicative inverse. The reciprocal of a nonzero number is the multiplicative inverse of that number. Reciprocal of x is 1/x.
x * 1/x = 1
Information Source: