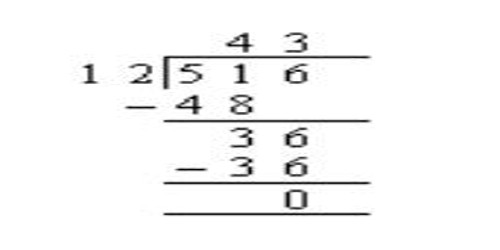Division without a Remainder
In mathematics, the remainder is the amount “left over” after performing some computation. How to divide a two digit number by a one digit number (e.g. 42 ÷ 7). Many long division problem ends in whole numbers (with no remainders).
Examples: 36 ÷ 4 = 9, 16 ÷ 4 = 4, 12 ÷ 4 = 3
Place the divisor (7) before the division bracket and place the dividend (42) under it.
Examine the first digit of the dividend (4). It is smaller than 7 so it can’t be divided by 7 to produce a whole number. Next take the first two digits of the dividend (42) and determine how many 7’s it contains. In this case 42 holds six sevens (6 * 7 = 42). Place the 6 above the division bracket.
Multiply the 6 by 7 and place the result (42) below the 42 of the dividend.
Draw a line under the 42 and subtract it from 42 (42 – 42=0). Since the result is 0 the division is finished and 6 is the answer.
When your division ends with a remainder, you must make sure that your remainder is less than your divisor. If your remainder is more than your divisor, you need to go back and check your division, because it is incorrect.
Explanation:
When you divide one number by another, sometimes the division is nice and even. Four (4) divided by two (2) gives you the quotient of two (2). But what happens if you divide five (5) by two (2)? Two goes into five two times, but then there is this pesky one (1) left over. That amount is called the remainder. You will get remainders when you are dividing whole numbers and you are not using decimal values in the quotients.
or basic math, you will have remainders. As you move forward in math and division, you will learn that remainders are only a starting point. You will eventually learn how to make decimals. Decimals allow you to write number values that are smaller than one. You might notice that we skipped the division problem of two (2) divided by three (3). We will get to values that are less than one in fractions and decimals.
Information Source: