Equally Inclined Lines
By the meaning of equally inclined lines, we mean that the lines which make equal angles with both the co-ordinate axes.
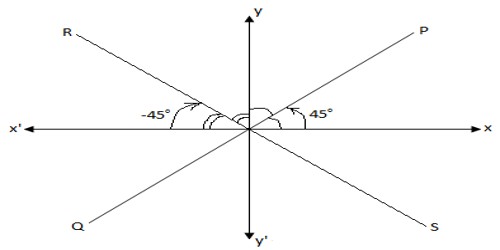
The above diagram shows that PQ and RS are the two equally inclined lines.
From the above diagram it is clear that;
For PQ: Inclination θ = 45°,
Therefore, slope = tan 45° = 1.
For RS: Inclination θ = -45°,
Therefore, slope = tan (-45°) = -1.
Lines and planes inclined toward or away from the picture plane have vanishing points similar to horizontal vanishing points. When constructing perspective drawings from plan and elevation views, locating the vanishing points for the inclined lines involves further preliminary projection.
Solved example on equally inclined lines:
Find the equation of the lines which is passes through the point (-2. 3) and equally inclined to the co-ordinate axes.
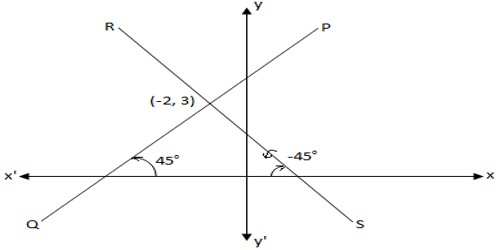
Solution:
From the above diagram it is clear that; there are two lines PQ and RS, equally inclined to the co-ordinate axes.
For line PQ: m = tan 45° = 1
and (x1, y1) = (-2, 3)
Therefore, its equation: y – y1 = m (x – x1)
⟹ y – 3 = 1 (x + 2)
⟹ y – 3 = x + 2
⟹ y = x + 5
For line RS: m = tan (-45°) = -1
and (x1, y1) = (-2, 3)
Therefore, its equation: y – y1 = m (x – x1)
⟹ y – 3 = -1(x + 2)
⟹ y – 3 = -x – 2
⟹ y = -x + 1
Therefore, the required equations are y = x + 5 and y = -x + 1
You can find the perspectives of inclined lines without finding the vanishing points by finding the perspectives of the end points and joining them. You can determine the perspective of any point by finding the perspectives of any two lines intersecting at the point.
Information Source: