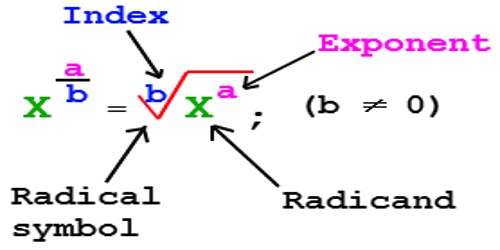
Evaluating Exponents of Positive and Negative Numbers
Exponents can be attached to variables as well as numbers. When they are, the basic rules of exponents and exponential notation apply when writing and simplifying algebraic expressions that contain exponents.
Any number or variable raised to a power of one is simply that number. In return, any number or variable that doesn’t have an exponent shown with it can be considered to have an exponent of 1. Below are some examples:
51 = 5
18 = 181
x1 = x
xy = x1 y1
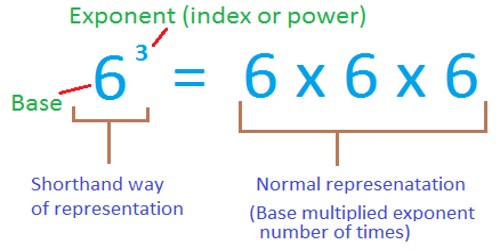
An exponent is a number that tells how many times the base number is used as a factor. For example, 34 indicates that the base number 3 is used as a factor 4 times. To determine the value of 34, multiply 3*3*3*3 which would give the result 81.
If a negative number is raised to an even power, the result will be positive.
(-2)4 = -2 * -2 * -2 * -2 = 16
A negative exponent just means that the base is on the wrong side of the fraction line, so you need to flip the base to the other side. For instance, “x–2” (pronounced as “ecks to the minus two”) just means “x2, but underneath, as in 1/x2.
If a negative number is raised to an odd power, the result will be negative.
(-2)5 = -2 * -2 * -2 * -2 * -2 = -32
The negative number must be enclosed by parentheses to have the exponent apply to the negative term.
Note that (-2)4 = -2 * -2 * -2 * -2 = 16
and -24 = -(2 * 2 * 2 * 2) = -16
Exponents are written as a superscript number (e.g. 34) or preceded by the caret (^) symbol (e.g. 3^4).
Some facts about exponents:
- Zero raised to any power is zero (e.g. 05 = 0)
- One raised to any power is one (e.g. 15 = 1)
- Any number raised to the zero power is one (e.g. 70 = 1)
- Any number raised to the first power is that number (e.g. 71 = 7)
Information Source: