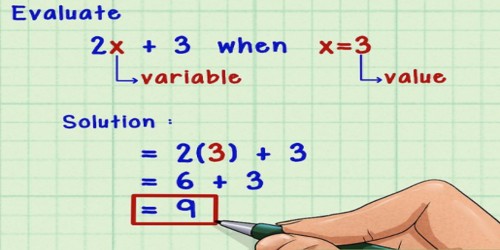Evaluating an Expression with Variable
A variable is a letter, for example x, y or z, that represents an unspecified number.
6+x=12
To evaluate an algebraic expression, you have to substitute a number for each variable and perform the arithmetic operations. In the example above, the variable x is equal to 6 since 6 + 6 = 12.
If we know the value of our variables, we can replace the variables with their values and then evaluate the expression.
Evaluating an Expression with One Variable
A mathematical expression can have a variable as part of the expression. If x=3, the expression 7x + 4 becomes 7 * 3 + 4 which is equal to 21 + 4 or 25. To evaluate an expression with a variable, simply substitute the value of the variable into the expression and simplify.
Evaluating an Expression with Two Variables
A mathematical expression can have variables as part of the expression. If x=3, and y=5, the expression 7x + y – 4 becomes 7 * 3 +5 – 4 which is equal to 21 + 5 – 4 or 22. To evaluate an expression with two or more variables, substitute the value of the variables into the expression and simplify.
Explanation
Here are the steps for evaluating an expression:
Replace each letter in the expression with the assigned value.
First, replace each letter in the expression with the value that has been assigned to it. To make your calculations clear and avoid mistakes, always enclose the numbers you’re substituting inside parentheses. The value that’s given to a variable stays the same throughout the entire problem, even if the letter occurs more than once in the expression.
However, since variables “vary”, the value assigned to a particular variable can change from problem to problem, just not within a single problem.
Perform the operations in the expression using the correct order of operations.
Once you’ve substituted the value for the letter, do the operations to find the value of the expression. Don’t forget to use the correct order of operations: first do any operations involving exponents, then do multiplication and division, and finally do addition and subtraction!
Here’s an example. Let’s evaluate the expression 2x3 – x2 + y for x = 3 and y = –2.
2(3)3 – (3)2 + (-2)
= 2(27) – 9 + (-2)
= 54 – 9 +(-2) = 43
Usually the only hard part in evaluation is in keeping track of the minus signs. I would strongly recommend that you use parentheses liberally, especially when you’re just getting started.
Evaluate a2b for a = –2, b = 3, c = –4, and d = 4.
To find my answer, you just plug in the given values, being careful to use parentheses, particularly around the minus signs:
(–2)2(3) = (4)(3) = 12
Information Source: