Finding the Fourth Angle of a Quadrilateral
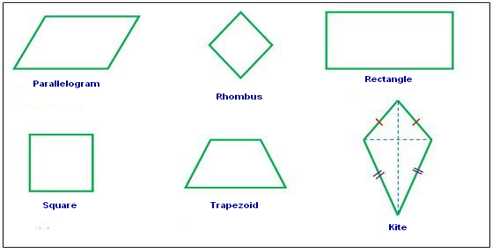
Quadrilaterals are four-sided polygons, with four vertexes, whose total interior angles add up to 360 degrees. A quadrilateral is any four-sided shape. These shapes also have exactly 4 interior angles. The sum of the interior angles of a quadrilateral is equal to 3600. That is, all 4 of the angles in a quadrilateral should add up to 3600. To find the fourth angle of a quadrilateral when the other three angles are known, subtract the number of degrees in the other three angles from 3600. The most common quadrilaterals are the rectangle, square, trapezoid, rhombus, and parallelogram.
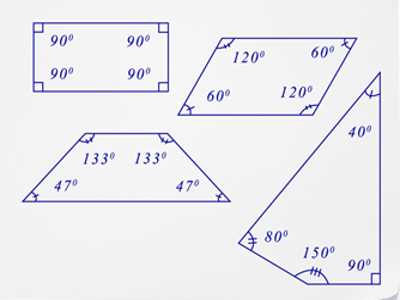
When three angles are known but the fourth is unknown, we can calculate the unknown angle. To find the fourth unknown angle of a quadrilateral, subtract the number of degrees in the other three angles from 360°.
Example: How many degrees are in the fourth angle of a quadrilateral whose other angles are 80°, 90°, and 65°?
Answer: 360° – 40° – 90° – 65° = 125°
Explanation
Three angles of a quadrilateral are 54°, 80°, and 116°. Find the measure of the fourth angle.
Solution,
Let the measure of the fourth angle be x°.
We know that the sum of the angles of a quadrilateral is 360°.
Therefore, 54 + 80 + 116 + x = 360
⇒ 250 + x = 360
⇒ x = (360 – 250) = 110.
Hence, the measure of the fourth angle is 110°.
Another one, the measures of two angles of a quadrilateral are 115°and 45°, and the other two angles are equal. Find the measure of each of the equal angles.
Solution,
Let the measure of each of the equal angles be x°.
We know that the sum of all the angles of a quadrilateral is 360°.
Therefore, 115 + 45 + x + x = 360
⇒ 160 + 2x = 360
⇒ 2x = (360 – 160) = 200
⇒ x = 100.
Hence, the measure of each of the equal angles is 100°.
Information Source;