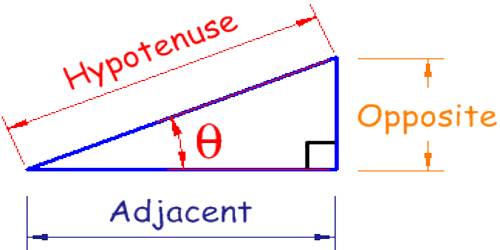
“Trigon” is Greek for the triangle, and “metric” is Greek for measurement. The trigonometric ratios are special measurements of a right triangle (a triangle with one angle measuring 90°). Remember that the two sides of a right triangle which form the right angle are called the legs, and the third side (opposite the right angle) is called the hypotenuse.
Two angles are complementary if the sum of their angles equals 900. A common case is when they form a right angle. If one angle is known, its complementary angle can be found by subtracting the measure of its angle from 900. Complementary angles form a right angle (L shape) and have a sum of 90 degrees.
Find out trigonometrical ratios of complementary angles
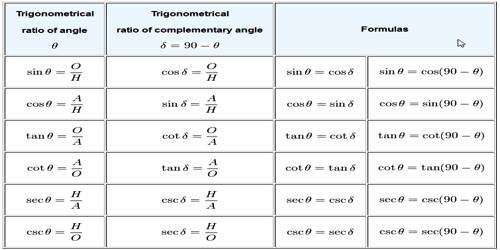
If the sum of two angles is one right angle or 90°, then one angle is said to be complementary to the other. Thus, 25° and 65°; θ° and (90 – θ)° are complementary to each other.
Suppose a rotating line rotates about O in the anti-clockwise sense and starting from its initial position
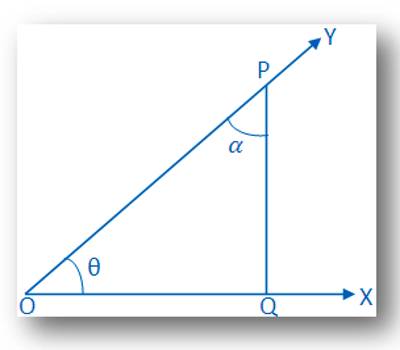
OX→ traces out angle ∠XOY = θ, where θ is acute.
Take a point P on OY→ and draw PQ perpendicular to OX. Let, ∠OPQ = α. Then, we have,
α + θ = 90°
or, α = 90° – θ.
Therefore, θ and α are complementary to each other.
Now, by the definition of trigonometric ratio,
sin θ = PQ/OP; ………. (i)
cos θ = OQ/OP; ………. (ii)
tan θ = PQ/OQ ………. (iii)
And sin α = OQ/OP; ………. (iv)
cos α = PQ/OP; ………. (v)
tan α = OQ/PQ ….… (vi)
From (i) and (iv) we have,
sin α = cos θ
or, sin (90° – θ) = cos θ;
From (ii) and (v) we have,
cos α = sin θ
or, cos (90° – θ) = sin θ;
From (iii) and (vi) we have,
And tan α = 1/tan θ
or, tan (90° – θ) = cot θ.
Similarly, csc (90° – θ) = sec θ;
sec (90° – θ) = csc θ
and cot (90° – θ) = tan θ.
Therefore,
Sine of any angle = cosine of its complementary angle;
Cosine of any angle = sine of its complementary angle;
The tangent of any angle = cotangent of its complementary angle.
Corollary:
Complementary Angles: Two angles are said to be complementary if their sum is 90°. Thus θ and (90° – θ) are complementary angles.
(i) sin (90° – θ) = cos θ
(ii) cos (90° – θ) = sin θ
(iii) tan (90° – θ) = cot θ
(iv) cot (90° – θ) = tan θ
(v) sec (90° – θ) = csc θ
(vi) csc (90° – θ) = sec θ
We know there are six trigonometrical ratios in trigonometry. The above explanation will help us to find the trigonometrical ratios of complementary angles.
Information Source: