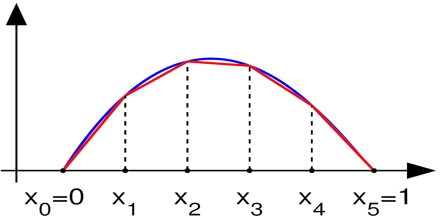
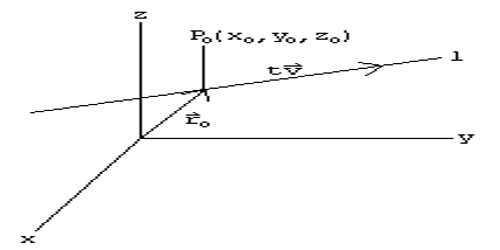
In mathematics, the finite element method (FEM) is a numerical technique intended for finding approximate solutions to boundary value problems for partial differential equations. It uses subdivision of a whole problem site into simpler parts, called finite aspects, and variational methods from the calculus of variations to resolve the problem by minimizing an affiliated error function.
Finite Element Method