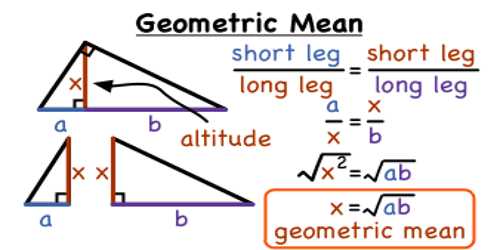
Geometric Mean
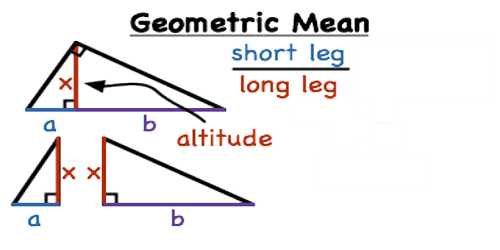
The geometric mean is a type of average, usually used for growth rates, like population growth or interest rates. While the arithmetic mean adds items, the geometric mean multiplies items. Also, you can only get the geometric mean for positive numbers. If three quantities are in Geometric Progression then the middle one is called the geometric mean of the other two.
It is not the same as the arithmetic mean, or average, that we know. For the arithmetic mean, we add our numbers together and divide by how many numbers we have. The geometric mean uses multiplication and roots. For example, for the product of two numbers, we would take the square root. For the product of three numbers, we take the third root.
Let, three numbers a, G and ‘b’ are in Geometric Progression then, the middle number G is called the geometric mean between two numbers a and b.
⇔ a, G, b, are in Geometric Progression
⇔ G/a = b/G = common ratio.
⇔ G2 = ab
⇔ G = ±√ab
Solved examples of Geometric Mean
- In the Geometric Progression {3, 9, 27}, 9 is the geometric mean of 3 and 27.
- The geometric mean between 3 and 12 is given by G = √(3 X 12) = √36 = 6
- The geometric mean between -3 and -27 is given by G =√(-3) X (-27) = – 9
Therefore, the geometric mean of two given quantities is any one of the two square root of their product.
When more than three quantities are in Geometric Progression then, the quantities between the two extremes are called the geometric means of the extreme quantities.
Therefore, in the Geometric Progression {4, 8, 16, 32, 64} the terms 8, 16 and 32 are the geometric means of the extreme terms 4 and 64.
Similarly, in the Geometric Progression {5, 15, 45, 135, 405, 1215, 3645} the terms 15, 45, 135, 405 and 1215 are the geometric means of the extreme terms 5 and 3645.
Example: What is the geometric mean of 2, 3, and 6?
First, multiply the numbers together and then take the cubed root (because there are three numbers) = (2*3*6)1/3 = 3.30
Note: the power of (1/3) is the same as the cubed root 3√. To convert an ‘nth’ root to this notation, just change the denominator in the fraction to whatever “n” you have. So:
5th root = to the (1/5) power
12th root = to the (1/12) power
99th root = to the (1/99) power.
Information Source;