In mathematics, a geometric progression (sequence) (also inaccurately known as a geometric series) is a sequence of numbers such that the quotient of any two successive members of the sequence is a constant called the common ratio of the sequence.
The geometric progression can be written as:
ar0 = a, ar1 = ar, ar2, ar3, … …
where r ≠ 0, r is the common ratio and a is a scale factor(also the first term).
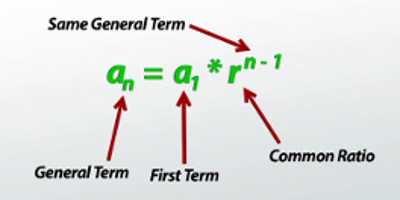
Different types of Geometric Progression formulae are pointed below;
(1) The general form of a Geometric Progression is {a, ar, ar2, ar3, ar4, …………}, where ‘a’ and ‘r’ are called the first term and common ratio of the Geometric Progression.
(2) The general term or nth term of a Geometric Progression with the first term ‘a’ and common ratio ‘r’ is given by tn = a ∙ rn – 1
(3) The sum of first n terms of the Geometric Progression whose first term ‘a’ and common ratio ‘r’ is given by
Sn = a [(rn − 1)/(r – 1)]
⇒ Sn = a(1 – rn), r ≠ 1.
(4) If x be the geometric mean of two given quantities a and b then, x = ± √ab.
When a and b are two quantities of opposite symbols then, the geometric mean between these quantities does not exist.
(5) (i) If the product of three numbers in Geometric Progression is given, assume the numbers as a/r, a and ar. Here the common ratio is r.
(ii) If the product of four numbers in Geometric Progression is given, assume the numbers as a/r3, a/r, ar and ar3. Here the common ratio is r2.
(iii) If the product of five numbers in Geometric Progression is given, assume the numbers as a/r2, a/r, a, ar and ar2. Here the common ratio is r.
(iv) If the product of the numbers is not given, then the numbers are taken as a, ar, ar2, ar3, ar4, ar5, ………………..
(6) A series of the form a + ar + ar2 + ar3…… + arn + …………… ∞ is called an infinite geometric series.
(7) The sum of an infinite Geometric mean, whose first term ‘a’ and common ratio ‘r’ (-1 < r < 1 i.e., |r| < 1) is; S = a / (1 − r)
i.e., If -1 < r < 1, then a + ar + ar2 + ar3 + ar4 + ………….. ∞ = a / (1 − r).
Information Source;