Geometrical Property of Altitudes
Sometimes the opposite side isn’t quite long enough to draw an altitude, so we are allowed to extend it to make an altitude possible. This line containing the opposite side is called the extended base of the altitude. The intersection of the extended base and the altitude is called the foot of the altitude.
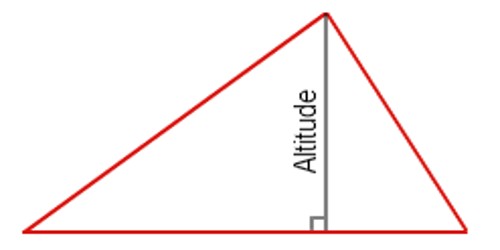
The distance between a vertex of a triangle and the opposite side is an altitude. Formally, the shortest line segment between a vertex of a triangle and the (possibly extended) opposite side.
The three altitudes of a triangle are concurrent. The point at which they intersect is known as the orthocentre of the triangle.
In the adjoining figure, the three altitudes XP, YQ, and ZR intersect at the orthocentre O.
In the adjoining figure ∆XYZ is a right-angled triangle. Here we see that XY ⊥ YZ, YZ ⊥ XY, and YM ⊥ XZ.
Thus, the three altitudes XY, YZ, and YM intersect at Y. So, Y is the orthocentre of ∆XYZ.
In an obtuse-angled ∆XYZ, the altitudes with respect to XY, YZ, and ZX are ZR, XP, and YQ respectively.
The altitudes when produced, meet at O. The O is the orthocentre of ∆XYZ.
We see that the orthocentre may lie within, on or outside the triangle.
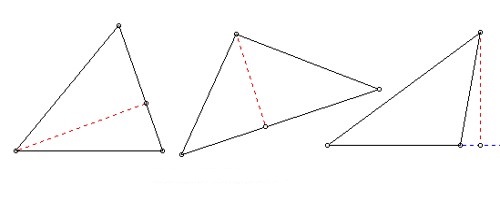
Fig: Property of Altitudes
The following points tell you about the length and location of the altitudes of the different types of triangles:
Scalene: None of the altitudes has the same length.
Isosceles: Two altitudes have the same length.
Equilateral: All three altitudes have the same length.
Acute: All three altitudes are inside the triangle.
Right: The altitude perpendicular to the hypotenuse is inside the triangle; the other two altitudes are the legs of the triangle (remember this when figuring the area of a right triangle).
Obtuse: The altitude connected to the obtuse vertex is inside the triangle, and the two altitudes connected to the acute vertices are outside the triangle.
Information Source;