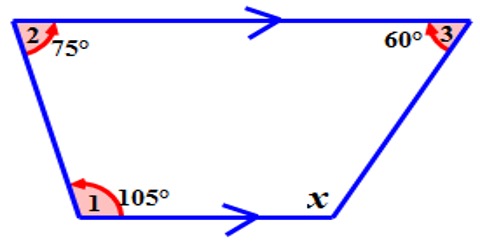
Finding the Fourth Angle of a Quadrilateral
Angles are measured in degrees, written °. The maximum angle is 360°. This is the angle all the way round a point. Half of this is the angle on a straight line, which is 180°. A quadrilateral is any four-sided shape. These shapes also have exactly 4 interior angles. The sum of the interior angles of a quadrilateral are equal to 360°. That is, all 4 of the angles in a quadrilateral should add up to 360°.
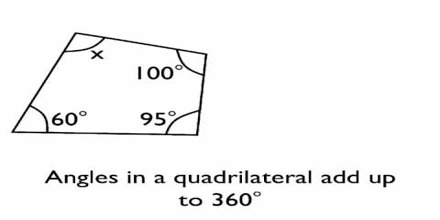
The sum of the interior angles of a quadrilateral are equal to 3600. To find the fourth angle of a quadrilateral when the other three angles are known, subtract the number of degrees in the other three angles from 3600.
Example: How many degrees are in the fourth angle of a quadrilateral whose other three angles are 800 and 1100 and 950? Answer: 3600 – 600 – 1000 – 950 = 1050
When three angles are known but the fourth is unknown, we can calculate the unknown angle. To find the fourth unknown angle of a quadrilateral, subtract the number of degrees in the other three angles from 360°.
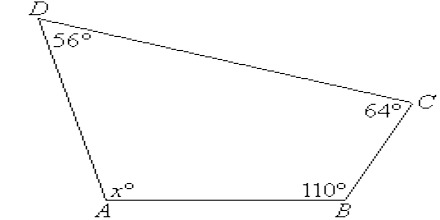
Example: Three angles of a quadrilateral are 54°, 80° and 116°. Find the measure of the fourth angle.
Solution:
Let the measure of the fourth angle be x°.
We know that the sum of the angles of a quadrilateral is 360°.
Therefore, 56 + 64 + 110 + x = 360
⇒ 230 + x = 360
⇒ x = (360 – 230) = 130.
Hence, the measure of the fourth angle is 130°.