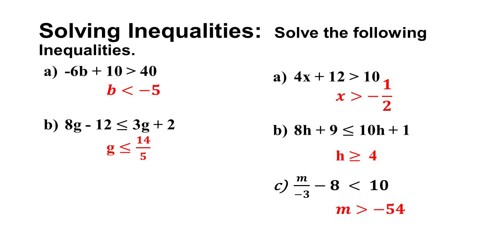How to Solve a Linear Inequation Algebraically?

How to Solve a Linear Inequation Algebraically?

A linear inequation is a linear expression that contains relational symbols. That means that instead of =, you’ll see >, <, >, or <. To solve a given linear inequation means to find the value or values of the variable used in it. Inequations that have the same solution are called equivalent. There are properties of inequalities as well as there were properties of equality. All the properties below are also true for inequalities involving ≥ and ≤.

Most of the rules or techniques involved in solving multi-step equations should easily translate to solving inequalities. The only big difference is how the inequality symbol switches direction when a negative number is multiplied or divided to both sides.

Thus; (i) to solve the inequation 4x + 7 > 23 means to find the variable x.

(ii) to solve the inequation 12 – 5y ≤ 17 means to find the variable y and so on.

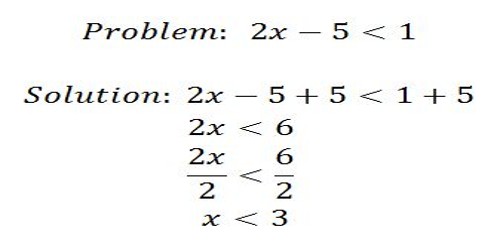
On the basis of the laws of the inequality, we have the following working rules:

I: Rule of transferring a positive term: If we transfer a positive term (the term in addition) from one side of an inequations to its other side, then the sign of the term becomes negative.

For example:

3x + 5 > 9 ⟹ 3x > 9 – 5
7x + 2 ≤ 29 ⟹ 7x ≤ 29 – 2
14 ≥ 3x + 11 ⟹14 – 11 ≥ 3x and so on.

II: Rule of transferring a negative term: If we transfer a negative term (the term in subtraction) from one side of an inequations to its other side, then the sign of the term becomes positive.

For example:

3x – 5 > 9 ⟹ 3x > 9 + 5
7x – 2 ≤ 29 ⟹ 7x ≤ 29 + 2
14 ≥ 3x – 11 ⟹14 + 11 ≥ 3x and so on.

III: Rule of multiplication/division by a positive number: If we multiply or divide by the same positive number to each term of an inequation then, the sign of inequality remains the same.

i.e., All terms on both sides of an inequality can be multiplied or divided by a positive number.

IV: Rule of multiplication/division by a negative number: If we multiply or divide by the same negative number to each term of an inequation then, the sign of inequality reverse.

i.e., All terms on both sides of an inequality can be multiplied or divided by a negative number on reversing the inequality. If we change the sign of each term on both sides of an inequation, then the sign of inequality gets reversed.

For example: