Hyperbola in Coordinate Geometry
Co-ordinates Geometry is a system of geometry where the position of points on the plane is described using an ordered pair of numbers. Straight lines in coordinate geometry are the same idea as in regular geometry, except that they are drawn on a coordinate plane and we can do more with them.
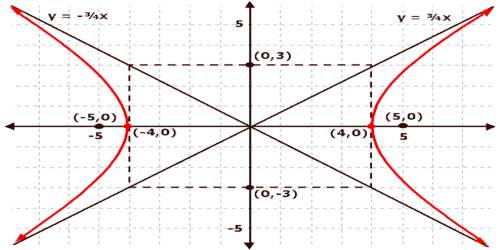
Hyperbola is asymmetrical open curve formed by the intersection of a circular cone with a plane at a smaller angle with its axis than the side of the cone. A hyperbola is a curve where the distances of any point from:
- a fixed point (the focus), and
- a fixed straight line (the directrix) is always in the same ratio.
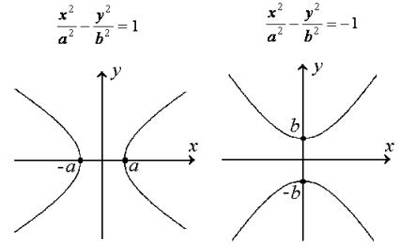
Hyperbola:
(i) Standard equation of hyperbola is x2/a2 – y2/b2 = 1 . . . (1)
(a) Its centre is the origin and transverse and conjugate axes are along x and y-axes respectively ; its length of transverse axis = 2a and that of conjugate axis = 2b and eccentricity = e = √[1 + (b2/a2)].
(b) If S and S’ be the two foci and P (x, y) any point on it then SP = ex – a, S’P = ex + a and S’P – SP = 2a.
(c) The point (x1, y1) lies outside, on or inside the hyperbola (1) according as x12/a2 – y12/b2 = -1 < , = or, > 0.
(d) The parametric equation of the hyperbola (1 ) are x = a sec θ, y = b tan θ and the parametric co-ordinates of any point P on (1) are (a sec θ,b tan θ).
(e) The equation of auxiliary circle of the hyperbola (1) is x2 + y2 = a2.
(ii) Other forms of the equations of hyperbola:
(a) y2/a2 – x2/b2 = 1.
Its centre is the origin and transverse and conjugate axes are along y and x-axes respectively.
(b) [(x – α)2]/a2 – [(y – β)2]/b2 = 1. Its centre is at (α, β) and transverse and conjugate axes are parallel to x-axis and y-axis respectively.
(iii) Two hyperbolas
x2/a2 – y2/b2 = 1 ………..(2) and y2/b2 – x2/a2 = 1 …….. (3)
are conjugate to one another. If e1 and e2 be the eccentricities of the hyperbolas (2) and (3) respectively, then
b2 = a2 (e12 – 1) and a2 = b2 (e22 – 1).
(iv) The equation of rectangular hyperbola is x2 – y2 = a2 ; its eccentricity = √2.
Information Source: