Introduction of locus – math:
The concept of locus – math is very important in analytical geometry.
The definitions of a plane curve like circle, parabola, ellipse etc. are based on the concept of the locus. So, a locus is a set of points satisfying a certain condition. For example, the locus of points that are 1cm from the origin is a circle of radius 1cm centered on the origin, since all points on this circle are 1cm from the origin.
Suppose X and Y are two fixed points in the two-dimensional coordinate plane. If a point M moves on this plane in such a manner that its distance from the points X and Y are always equal, then the point M will trace out a definite path on the plane.
Again, if the point M moves path on the plane in such a manner that MX² + MY² = 36, then the moving point M will trace out another definite path on the plane.
Thus, a moving point M trace out a definite path on the given plane if it satisfies some specified geometrical conditions. Such a path traced out by a moving point M on a plane is called its locus.
For example, the locus of points in the plane equidistant from a given point is a circle, and the set of points in three-space equidistant from a given point is a sphere.
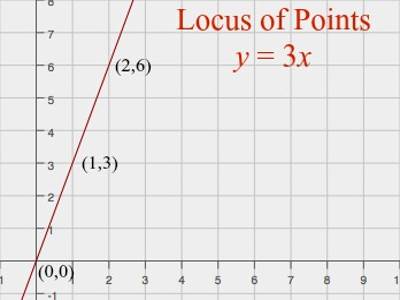
The word locus describes the position of points which obey a certain rule.
Three important loci are:
- The circle – the locus of points which are equidistant from a fixed point, the center.
- The perpendicular bisector – the locus of points which are equidistant from two fixed points A and B.
- The angle bisector – the locus of points which are equidistant from two fixed lines.
Information Source: