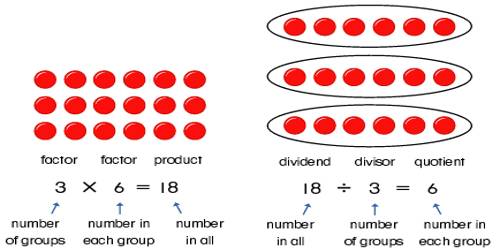
Inverse Relationship between Multiplication and Division
The inverse relationship is a relationship between two numbers in which an increase in the value of one number results in a decrease in the value of the other number. The inverse relationship is also known as negative correlation in regression analysis; this means that when one variable increases, the other variable decreases, and vice versa.
Multiplication and Division Relationship
There is an inverse relationship between multiplication and division just like there was between addition and subtraction.
The equation 3 * 7 = 21 has the inverse relationships:
- 21 ÷ 3 = 7
- 21 ÷ 7 = 3
Similar relationships exist for the division. The equation 45 ÷ 5 = 9 has the inverse relationships:
- 5 * 9 = 45
- 9 * 5 = 45

Explanation
A multiplicative inverse is reciprocal. What is a reciprocal? A reciprocal is one of a pair of numbers that when multiplied by another number equals the number 1. For example, if we have the number 7, the multiplicative inverse, or reciprocal, would be 1/7 because when you multiply 7 and 1/7 together, you get 1!
Examples
Let’s look at a couple examples before proceeding with the lesson.
Example 1: What is the multiplicative inverse of 15? In other words, which number, when multiplied with 15, would give us the number 1 as a result? Let’s solve this in an algebraic way, with x being the unknown multiplicative inverse.
15 * x = 1
x = 1/15
That’s it! It was really that simple! The multiplicative inverse of a number is that number as the denominator and 1 as the numerator. When we multiply 15 and 1/15, we get 1.
Example 2: What is the multiplicative inverse of 1/4? Now, this example is a little different because we are beginning with a fraction. Let’s again solve this algebraically, with x being the unknown multiplicative inverse of 1/4.
1/4 * x = 1
x = 1 / (1/4)
(1/1) / (1/4) = (1/1) * (4/1) = 4
Remember that when you divide fractions, you must flip the numerator and denominator of the second fraction and then multiply. We got 4 as the multiplicative inverse of 1/4. Makes sense, right?
So, the conclusion that we can draw from these two examples is that when you have a whole number, the multiplicative inverse of that number will be that number in fraction form with the whole number as the denominator and 1 as the numerator. When you have a fraction with 1 as the numerator, the multiplicative inverse of that fraction will simply be the denominator of the fraction.
Information Source: