An irrational number cannot be expressed as a ratio between two numbers and it cannot be written as a simple fraction because there is not a finite number of numbers when written as a decimal. Instead, the numbers in the decimal would go on forever, without repeating. An Irrational Number is a real number that cannot be written as a simple fraction. Example: 1.5 is rational, because it can be written as the ratio 3/2.
The most famous irrational number is √2, sometimes called Pythagoras’s constant. Legend has it that the Pythagorean philosopher Hippasus used geometric methods to demonstrate the irrationality of √2 while at sea and, upon notifying his comrades of his great discovery, was immediately thrown overboard by the fanatic Pythagoreans. Other examples include √3, e, π, etc.
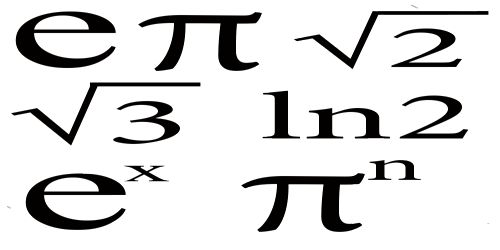
Common Examples of Irrational Numbers
Pi, which begins with 3.14, is one of the most common irrational numbers. Pi is determined by calculating the ratio of the circumference of a circle (the distance around the circle) to the diameter of that same circle (the distance across the circle). Pi has been calculated to over a quadrillion decimal places, but no pattern has ever been found; therefore it is an irrational number.
√2/3; although this number can be expressed as a fraction, we need more than that, for the number to be rational. The fraction’s numerator and denominator must both be integers, and 2–√2 cannot be expressed as an integer.
Irrational Numbers are numbers that cannot be expressed as a ratio between two integers and is not an imaginary number. If written in decimal notation, an irrational number would have an infinite number of digits to the right of the decimal point, without repetition. Pi and the square root of 2 (√2) are irrational numbers.

Applications of irrational numbers:
In compound interest: Let us have a look at the following example to understand how irrational number helps us in case of calculating compound interest:
An amount of Rs. 2,00,000 is given to Animesh by his friend for a tenure of 2 years at interest of 2% per annum compounded annually. Calculate the amount which Animesh needs to return his friend after 2 years.
Solution:
Principal = Rs 2,00,000
Time = 2 years
Interest rate (r) = 2% p.a.
Amount = p (1 + r/100)t
So, amount = 2,00,000 (1 + 2/100)2
= 2,00,000 (102/100)2
= 2,08,080
Hence, the amount that Animesh needs to return to his friend is Rs. 2,08,080.
So, compound interest is one of the applications of irrational numbers where we use sum of infinite series.
Information Source:
- Only Math