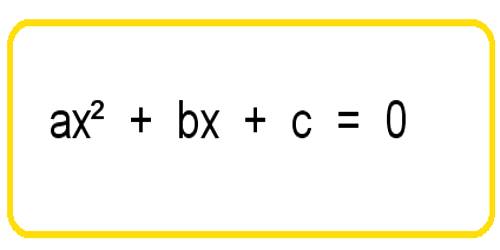A polynomial of the second degree is generally called a quadratic polynomial. In elementary algebra, the quadratic formula is the solution of the quadratic equation. There are other ways to solve the quadratic equation instead of using the quadratic formula, such as factoring, completing the square, or graphing. Using the quadratic formula is often the most convenient way.
If f(x) is a quadratic polynomial, then f(x) = 0 is called a quadratic equation.
An equation in one unknown quantity in the form ax2 + bx + c = 0 is called quadratic equation.
A quadratic equation is an equation of the second degree.
Irrational Roots of a Quadratic Equation
In a quadratic equation with rational coefficients has an irrational or surd root α + √β, where α and β are rational and β is not a perfect square, then it has also a conjugate root α – √β.
Proof:
To prove the above theorem let us consider the quadratic equation of the general form:
ax2 + bx + c = 0 where, the coefficients a, b and c are real.
Let p + √q (where p is rational and √q is irrational) be a surd root of equation ax2 + bx + c = 0. Then the equation ax2 + bx + c = 0 must be satisfied by x = p + √q.
Therefore,
a(p + √q)2 + b(p + √q) + c = 0
⇒ a(p2 + q + 2p√q) + bp + b√q + c = 0
⇒ ap2 – aq + 2ap√q + bp + b√q + c = 0
⇒ ap2 – aq + bp + c + (2ap + b)√q = 0
⇒ ap2 – aq + bp + c + (2ap + b)√q = 0 + 0 ∙ √q
Therefore,
ap2 – aq + bp + c = 0 and 2ap + b = 0
Now substitute x by p – √q in ax22 + bx + c we get,
a(p – √q)2 + b(p – √q) + c
= a(p2 + q – 2p√q) + bp – p√q + c
= ap2 + aq – 2ap√q + bp – b√q + c
= ap2 + aq + bp + c – (2ap + b)√q
= 0 – √q ∙ 0 [Since, ap2 – aq + bp + c = 0 and 2ap + b = 0] = 0
Now we clearly see that the equation ax2 + bx + c = 0 is satisfied by x = (p – √q) when (p + √q) is a surd root of the equation ax2 + bx + c = 0. Therefore, (p – √q) is the other surd root of the equation ax2 + bx + c = 0.
Similarly, if (p – √q) is a surd root of equation ax2 + bx + c = 0 then we can easily proved that its other surd root is (p + √q).
Thus, (p + √q) and (p – √q) are conjugate surd roots. Therefore, in a quadratic equation surd or irrational roots occur in conjugate pairs.
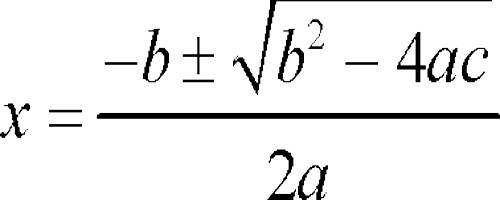
Solved example to find the irrational roots occur in conjugate pairs of a quadratic equation:
Find the quadratic equation with rational coefficients which has 2 + √3 as a root.
Solution:
According to the problem, coefficients of the required quadratic equation are rational and its one root is 2 + √3. Hence, the other root of the required equation is 2 – √3 (Since the surd roots always occur in pairs, so another root is 2 – √3.
Now, the sum of the roots of the required equation = 2 + √3 + 2 – √3 = 4
And, product of the roots = (2 + √3)( 2 – √3) = 22 – (√3)22 = 4 – 3 = 1
Hence, the equation is
x2 – (Sum of the roots)x + product of the roots = 0
i.e., x2 – 4x + 1 = 0
Therefore, the required equation is x – 4x + 1 = 0.
Information Source: