Linear Inequalities in One Variable
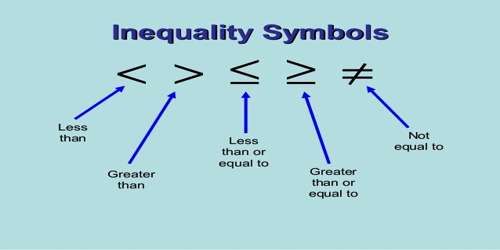
The mathematical statement which says that one quantity is not equal to another quantity is called an inequality. As the word “inequality” indicates something that is not equal, an algebraic inequality refers to an algebraic expression that is not equal to another. In an inequality, two expressions are either less than (or equal to) or greater than (or equal to) another expression.
A linear inequality is a mathematical statement that relates a linear expression as either less than or greater than another. The following are some examples of linear inequalities..
For example: If m and n are two quantities such that m ≠ n; then any one of the following relations (conditions) will be true:
i.e., either
(i) m > n
(ii) m ≥ n
(iii) m < n
Or, m ≤ n
Each of the four conditions, given above, is an inequality.
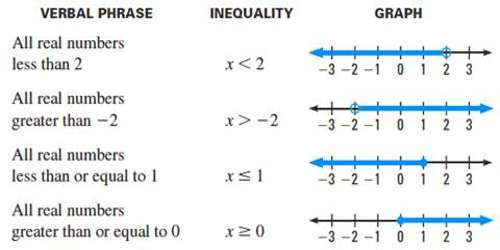
A solution to a linear inequality is a real number that will produce a true statement when substituted for the variable. Linear inequalities have either infinitely many solutions or no solution. If there are infinitely many solutions, graph the solution set on a number line and/or express the solution using interval notation.
Two permissible rules:
Addition — Subtraction Rule: If the same number or expression is added to or subtracted from both sides of an inequation, the resulting inequation has the same solution (or solutions) as the original.
Multiplication — Division Rule:
(i) If both sides of an inequation are multiplied or divided by the same positive number, the resulting inequation has the same solution (or solutions) as the original.
(ii) If both sides of an inequation are multiplied or divided by the same negative number, the resulting inequation has the same solution (or solutions) as the original if the symbol of the inequality is reversed. Thus, the only difference between solving a linear equation and solving an inequation concerns multiplying or dividing both sides by a negative number. Therefore, always reverse the symbol of an inequation when multiplying or dividing by a negative number.
Consider the following statement:
“x is a number which when added to 2 gives a sum less than 6.”
The above sentence can be expressed as x + 2 < 6, where ‘<’ stands for “is less than”.
x + 2 < 6 is a linear inequality in one variable, x.
Clearly, any number less than 4 when added to 2 has a sum less than 6.
So, x is less than 4.
We say that the solutions of the inequality x + 2 < 6 are x < 4.
The form of a linear inequality in one variable is ax + b < c, where a, b and c are fixed numbers belonging to the set R.
If a, b and c are real numbers, then each of the following is called a linear inequality in one variable:
Similarly, ax + b > c (‘>’ stands for “is greater than”)
ax + b ≥ c (‘≥’ stands for “is greater than or equal to”)
ax + b ≤ c (‘≤’ stands for “is less than or equal to”)
are linear inequation in one variable. In an inequation, the signs ‘>’, ‘<’, ‘≥’ and ‘≤’ are called signs of inequality.
Information Source: