Mathematics Logarithms
In mathematics, logarithms were developed for making complicated calculations simple. In mathematics, the logarithm is the inverse operation to exponentiation, just as division is the inverse of multiplication and vice versa. That means the logarithm of a number is the exponent to which another fixed number, the base, must be raised to produce that number.
For example, if a right circular cylinder has radius r = 0.375 meters and height h = 0.2321 meters, then its volume is given by: V = A = πr2h = 3.146 × (0.375)2 × 0.2321. Use of logarithm tables makes such calculations quite easy. However, even calculators have functions like multiplication; power etc. still, logarithmic and exponential equations and functions are very common in mathematics.
Definition:
If ax = M (M > 0, a > 0, a ≠ 1), then x (i.e., index of the power) is called the logarithm of the number M to the base ‘a’ and is written as x = loga M.
Hence, if ax = M then x = loga M;
conversely, if x = loga M then ax = M.
If ‘a’ is a positive real number (except 1), n is any real number and an = b, then n is called the logarithm of b to the base a. It is written as loga b (read as a log of b to the base a). Thus,
an = b ⇔ loga b = n.
an is called the exponential form and loga b = n is called the logarithmic form.
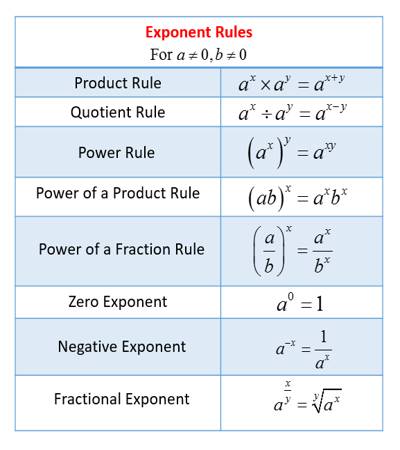
For example:
- 32 = 9 ⇔ log3 9 = 2
- 54 = 625 ⇔ log5 625 = 4
- 70 = 1 ⇔ log7 1 = 0
- 2-3 = 1/8 ⇔ log2 (1/8) = -3
- 10-2 = 0.01 ⇔ log10 0.01 = -2
- 2 = 64 ⇔ log 64 = 6
- 3-4 = 1/34 = 1/81 ⇔ log3 1/81 = -4
- 10-2 = 1/100 = 0.01 ⇔ log10 0.01 = -2
Notes on basic Logarithm Facts:
- Since a > 0 (a ≠ 1), an > 0 for any rational n. Hence logarithm is defined only positive real numbers.
From the definition, it is clear that the logarithm of a number has no meaning if the base is not mentioned.
- The above examples show that the logarithm of a (positive) real number may be negative, zero or positive.
- Logarithmic values of a given number are different for different bases.
- Logarithms to the base a 10 are called common logarithms. Also, logarithm tables assume base 10. If no base is given, the base is assumed to be 10.
For example, log 21 means log10 21.
- Logarithm to the base ‘e’ (where e = 2.7183 approx.) is called natural logarithm and is usually written as ln. Thus ln x means loge x.
- If ax = – M (a > 0, M > 0), then the value of x will be imaginary i.e., logarithmic value of a negative number is imaginary.
- A logarithm of 1 to any finite non-zero base is zero.
Proof: We know, a0 = 1 (a ≠ 0). Therefore, from the definition, we have, loga 1 = 0.
- The logarithm of a positive number to the same base is always 1.
Proof: Since a1 = a. Therefore, loga a = 1.
Information Source;