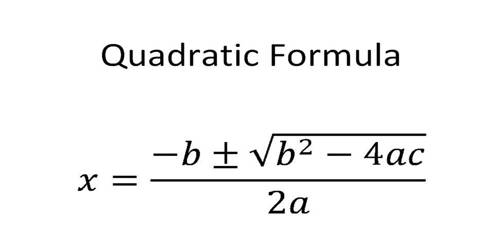A polynomial of the second degree is generally called a quadratic polynomial. In elementary algebra, the quadratic formula is the solution of the quadratic equation. There are other ways to solve the quadratic equation instead of using the quadratic formula, such as factoring, completing the square, or graphing. Using the quadratic formula is often the most convenient way.
If f(x) is a quadratic polynomial, then f(x) = 0 is called a quadratic equation.
An equation in one unknown quantity in the form ax2 + bx + c = 0 is called quadratic equation.
Maximum and Minimum Values of the Quadratic Expression
We will learn how to find the maximum and minimum values of the quadratic Expression ax2 + bx + c (a ≠ 0).
When we find the maximum value and the minimum value of ax2 + bx + c then let us assume y = ax2 + bx + c.
Or, ax2 + bx + c – y = 0
Suppose x is real then the discriminate of equation ax2 + bx + c – y = 0 is ≥ 0
i.e., b2 – 4a(c – y) ≥ 0
Or, b2 – 4ac + 4ay ≥ 0
4ay ≥ 4ac – b2
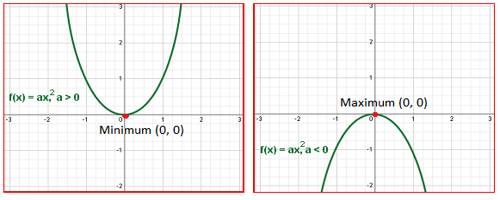
Case I: When a > 0
When a > 0 then from 4ay ≥ 4ac – b2 we get, y ≥ 4ac – b2/4a
Therefore, we clearly see that the expression y becomes minimum when a > 0
Thus, the minimum value of the expression is 4ac – b2/4a.
Now, substitute y = 4ac – b2/4a in equation ax2 + bx + c – y = 0 we have,
ax2 + bx + c – (4ac – b2/4a) = 0
or, 4a2x2 + 4abx + b2 = 0
or, (2ax + b)2 = 0
or, x = -b/2a
Therefore, we clearly see that the expression y gives its minimum value at x = -b/2a
Case II: When a < 0
When a < 0 then from 4ay ≥ 4ac – b2 we get,
y ≤ 4ac – b2/4a
Therefore, we clearly see that the expression y becomes maximum when a < 0.
Thus, the maximum value of the expression is 4ac – b2/4a.
Now substitute y = 4ac – b^2/4a in equation ax2 + bx + c – y = 0 we have,
ax2 + bx + c -(4ac – b2/4a) =0
or, 4a2x2 + 4abx + b2 = 0
or, (2ax + b)2 = 0
or, x = -b/2a.
Therefore, we clearly see that the expression y gives its maximum value at x = -b/2a.
Information Source: