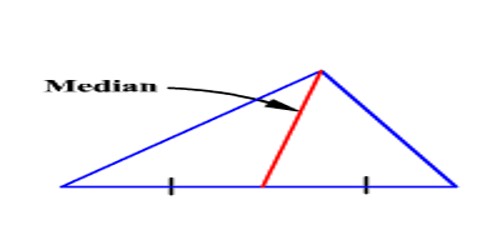
Medians of a Triangle
A median of a triangle is a line segment joining a vertex to the midpoint of the opposite side. Triangle is a plane figure with three straight sides and three angles. The three angles always add to 180°. The vertex is a corner of the triangle. Every triangle has three vertices. The interior angles of a triangle always add up to 180°. The exterior angles of a triangle always add up to 360°.
The straight line joining a vertex of a triangle to the midpoint of the opposite side is called a median. A triangle has three medians, one from each vertex, and they all intersect each other at the triangle’s centroid. Here XL, YM and ZN are medians.
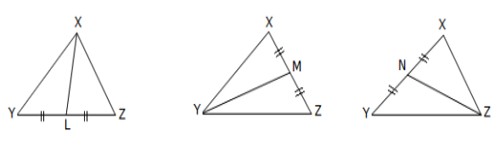
Fig: Medians of a Triangle
A geometrical property of medians:
The three medians of a triangle are concurrent, i.e., they have a common point of intersection. This point is known as the centroid of the triangle. It divides each median into the ratio 2 : 1.
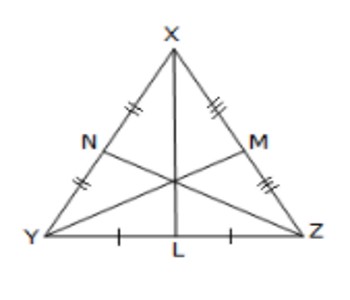
Fig: a geometrical property of medians
Here, the three medians intersect at G.
Thus, G is the centroid of the triangle.
Also, XG : GL = 2 : 1
YG : GM= 2 : 1
and ZG : GN = 2 : 1
There are some fascinating properties of the medians of a triangle:
- The fact that the three medians always meet at a single point is interesting in its own right
- Each median divides the triangle into two smaller triangles which have the same area
- The centroid (a point where they meet) is the center of gravity of the triangle
- The three medians divide the triangle into 6 smaller triangles that all have the same area, even though they may have different shapes.
- In the case of equilateral and isosceles triangles, a median bisects any angle at a vertex whose two adjacent sides are equal in length.
Information Source: