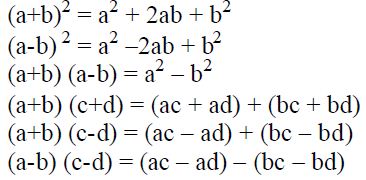Mental Math with Tricks and Shortcuts
Addition
Technique: Add left to right
326 + 678 + 245 + 567 = 900, 1100, 1600, 1620, 1690, 1730, 1790, 1804, & 1816
Note: Look for opportunities to combine numbers to reduce the number of steps to the solution. This was done with 6+8 = 14 and 5+7 = 12 above. Look for opportunities to form 10, 100, 1000, and etc. between numbers that are not necessarily next to each other. Practice!
Multiplication & Squaring
Some useful formulae Examples
(a+b)2 = a2 + 2ab + b2 492 = (40 + 9) 2 = 1600 + 720 + 81 = 2401
(a-b) 2 = a2 –2ab + b2 562 = (60 – 4) 2 = 3600 – 480 + 16 = 3136
(a+b) (a-b) = a2 – b2 64 x 56 = (60 – 4) (60 + 4) = 3600 – 16 = 3584
(a+b) (c+d) = (ac + ad) + (bc + bd) 23 x 34 = (20 + 3) (30 + 4) = 600 + 80 + 90 + 12 = 782
(a+b) (c-d) = (ac – ad) + (bc – bd) 34 x 78 = (30 + 4) (80 – 2) = 2400 –60 + 320 – 8 = 2652
(a-b) (c-d) = (ac – ad) – (bc – bd) 67 x 86 = (70 – 3) (90 – 4) = 6300 – 280 – 270 + 12 = 5762
X = 1 to 9 & Y = Any Number
(X5) 2 = 100X(X+1) + 25 652 = 600(7) + 25 = 4200 + 25 = 4225
25 x Y = (Y x 100)/4 25 x 76 = 7600/4 = 1900
50 x Y = (Y x 100)/2 50 x 67 = 6700/2 = 3350
75 x Y = 3(Y x 100)/4 75 x 58 = (5800 x 3)/4 = 17400/4 = 4350
Square any Two Digit Number (a = 10’s digit & b = 1’s digit)
(ab)2 = 100a2 + 20(a x b) + b2 672 = 100(36) + 20(42) + 49 = 4489
Multiply any Two 2 Digit Numbers (a & c = 10’s digit, b & d = 1’a digit)
ab x cd = 100(a x c) + 10[(b x c) + (a x d)] + (b x d) 53 x 68 = 3000 + 580 + 24 = 3604
Tricks using (X5) 2
(X5 – a) 2 = (X5) 2 – X5(2a) + a2) 632 = (65 – 2) 2 = 4225 – 260 + 4) = 3969
(X5 + a) 2 = (X5) 2 + X5(2a) + a2) 672 = (65 + 2) 2 = 4225 + 260 + 4) = 4489
Squaring Numbers 52 to 99
a2 = [a – (100 – a)]100 + (100 – a) 2 932 = (93 – 7)100 + 72 = 8649
Squaring Numbers 101 to 148
a2 = [a + (a – 100)]100 + (a – 100) 2 1082 = (108 + 8)100 + 82 = 11664
Squaring Numbers near 1000
a2 = [a – (1000 – a)]1000 + (1000 – a) 2 9942 = (994 – 6)1000 + 6 2 = 988036
a2 = [a + (a – 1000)]1000 + (a – 1000) 2 10072 = (1007 + 7)1000 + 72 = 1014049
Squaring Numbers that end in 1
a2 = (a – 1) 2 + 2a – 1 61 2 = 60 2 + 122 – 1 = 3600 + 121 = 3721
Squaring Numbers that end in 4
a2 = (a + 1)2 – (2a + 1) 442 = 452 – (88 + 1) = 2025 – 89 = 1936
Squaring Numbers that end in 6
a2 = (a – 1)2 + (2a – 1) 562 = 552 + 112 – 1 = 3025 + 111 = 3136
Squaring Numbers that end in 9
a2 = (a + 1) 2 – (2a + 1) 792 = 802 – (158 + 1) = 6400 – 159 = 6341
Using Squares to Help Multiply
Two Numbers that Differ by 1
If a > b then a x b = a2 – a 35 x 34 = 1225 – 35 = 1190
If a < b then a x b = a2 + a 35 x 36 = 1225 + 35 = 1260
Two Numbers that Differ by 2
a x b = [(a + b)/2]2 -1 26 x 28 = 272 -1 = 729 – 1 = 728
Two Numbers that Differ by 3 (a < b)
a x b = (a + 1)2 + (a – 1) 26 x 29 = 272 + 25 = 729 + 25 = 754
Two Numbers that Differ by 4
a x b = [(a + b)/2]2 – 4 64 x 68 = 662 – 4 = 4356 – 4 = 4352
Two Numbers that Differ by 6
a x b = [(a + b)/2]2 – 9 51 x 57 = 542 – 9 = 2916 – 9 = 2907
Two Numbers that Differ by an Even Number: a < b and c = (b – a)/2
a x b = [(a + b)/2]2 – c2 59 x 67 = 632 – 42 = 3969 – 16 = 3953
Two Numbers that Differ by an Odd Number: a < b and c = [1 + (b – a)]/2
a x b = (a + c)2 – [b + (c –1)2] 79 x 92 = 862 – (92 + 36) = 7396 – 128 = 7268
Other Multiplying Techniques
Multiplying by 11
a x 11 = a + 10a 76 x 11 = 76 + 760 = 836
a x 11 = If a > 9 insert a 0 between digits and
add sum of digits x 10 76 x 11 = 706 + 130 = 836
Multiplying by Other Two Digit Numbers Ending in 1 (X = 1 to 9)
a x X1 = a + X0a 63 x 41 = 63 + (40 x 63) = 63 + 2520 = 2583
Multiplying with Numbers Ending in 5 (X = 1 to 9)
a x X5 = a/2 x 2(X5) 83 x 45 = 41.5 x 90 = 415 x 9 = 3735
Multiplying by 15
a x 15 = (a + a/2) x 10 77 x 15 = (77 + 38.5) x 10 = 1155
Multiplying by 45
a x 45 = 50a – 50a/10 59 x 45 = 2950 – 295 = 2655
Multiplying by 55
a x 55 = 50a + 50a/10 67 x 55 = 3350 + 335 = 3685
Multiplying by Two Digit Numbers that End in 9 (X = 1 to 9)
a x X9 = (X9 + 1)a – a 47 x 29 = (30 x 47) – 47 = 1410 – 47 = 1363
Multiplying by Multiples of 9 (b = multiple of 9 up to 9 x 9)
a x b = round b up to next highest 0 29 x 54 = 29 x 60 – (29 x 60)/10 = 1740 – 174 = 1566
multiply then subtract 1/10 of result
Multiplying by Multiples of 99 (b = multiple of 99 up to 99 x 10)
a x b = round up to next highest 0 38 x 396 = 38 x 400 – (38 x 400)/100 = 15200 – 152 = 15048
multiply and then subtract 1/100 of result
SUBTRACTION
Techniques:
1) Learn to calculate from left to right: 1427 – 698 = (800 – 100) + (30 – 10) + 9 = 729
2) Think in terms of what number added to the smaller equals the larger: 785 – 342 = 443 (left to right)
3) Add a number to the larger to round to next highest 0; then add same number to the smaller and subtract:
496 – 279 = (496 + 4) – (279 + 4) = 500 – 283 = 217 (left to right)
4) Add a number to the smaller to round to the next highest 10, 100, 1000 and etc.; then subtract and add
the same number to the result to get the answer: 721 – 587 = 721 – (587 + 13) = (721 – 600) + 13 = 134
5) Subtract a number from each number and then subtract: 829 – 534 = 795 – 500 = 295
DIVISION
Techniques: Examples
Divide by parts of divisor one at a time: 1344/24 = (1344/6)/4 = 224/4 = 56
Method of Short Division
340 ————— Remainders (3, 4, and 0 during calculations)
7)1792
256 ———————Answer
Divide both divisor and dividend by same number to get a short division problem
10
972/27 divide both by 9 = 3)108
36
Dividing by 5, 50, 500, and etc.: Multiply by 2 and then divide by 10, 100, 1000, and etc.
365/5 = 730/10 = 73
Dividing by 25, 250, 2500, and etc.: Multiply by 4 and divide by 100, 1000, 10000, and etc.
Dividing by 125: Multiply by 8 and then divide by 1000
36125/125 = 289000/1000 = 289
It can be divided evenly by:
2 if the number ends in 0, 2, 4, 6, and 8
3 if the sum of the digits in the number is divisible by 3
4 if the number ends in 00 or a 2 digit number divisible by 4
5 if the number ends in 0 or 5
6 if the number is even and the sum of the digits is divisible by 3
7 sorry, you must just try this one
8 if the last three digits are 000 or divisible by 8
9 if the sum of the digits are divisible by 9
10 if the number ends in 0
11 if the number has an even number of digits that are all the same: 33, 4444, 777777, and etc.
11 if, beginning from the right, subtracting the smaller of the sums of the even digits and odd digits
results in a number equal to 0 or divisible by 11:
406857/11 Even = 15 Odd = 15 = 0
1049807/11 Even = 9 Odd = 20 = 11
12 if test for divisibility by 3 & 4 work
15 if test for divisibility by 3 & 5 work
Others by using tests above in different multiplication combinations
USE ESTIMATES
Use estimates to check your answers. Get in the habit of doing this for all calculations.