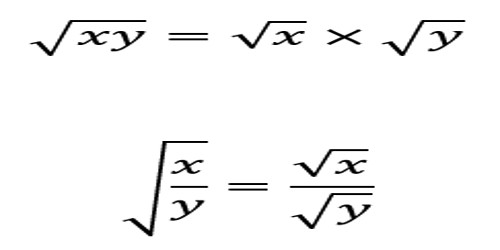Order of a Surd
Definitions of surds: A root of a positive real quantity is called a surd if its value cannot be exactly determined. It is a number that can’t be simplified to remove a square root (or cube root etc). For example, each of the quantities √3, ∛7, ∜19, (16)^2/5 etc. is a surd.
More Examples:
- √2 (square root of 2) can’t be simplified further so it is a surd
- √4 (square root of 4) CAN be simplified to 2, so it is NOT a surd
The order of a surd indicates the index of root to be extracted.
In a√n, n is called the order of the surd and a is called the radicand.
For example, The order of the surd 5√z is 5.
(i) A surd with an index of root 2 is called a second order surd or quadratic surd.
Example: √2, √5, √10, √a, √m, √x, √(x + 1) are second-order surd or quadratic surd (since the indices of roots are 2).
(ii) A surd with an index of root 3 is called a third order surd or cubic surd.
Example: ∛2, ∛5, ∛7, ∛15, ∛100, ∛a, ∛m, ∛x, ∛(x – 1) are third order surd or cubic surd (since the indices of roots are 3).
(iii) A surd with an index of root 4 is called a fourth order surd.
Example: 4√2, 4√3, 4√9, 4√17, 4√70, 4√a, 4√m, 4√x, 4√(x-1) are third order surd or cubic surd (since the indices of roots are 4).
(iv) In general, a surd with an index of root n is called an nth order surd.
Example: n√2, n√3, n√9, n√17, n√70, n√a, n√m, n√x, n√(x-1) are nth order surd (since the indices of roots are n).
Problem on finding the order of a surd:
Express ∛4 as a surd of order 12.
Solution:
Now, ∛4
= 41/3
= 44^(1×4)/(3×4), [Since we are to convert order 3 into 12, so we multiply both a numerator and denominator of 1/3 by 4]
= 44/12 = 12√44 = 12√256.
Information Source: