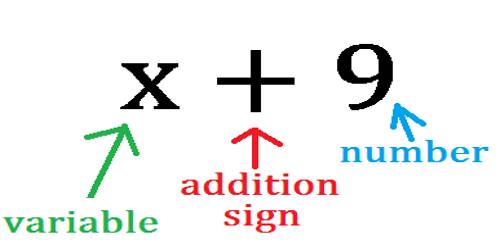
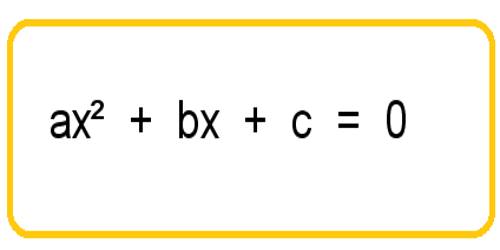Position of a Point in a Plane
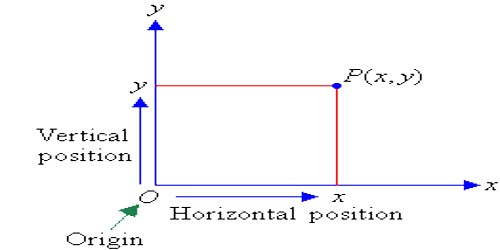
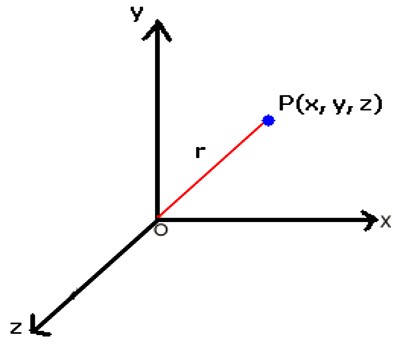
We know that the position of a point in a plane is given by its coordinates.
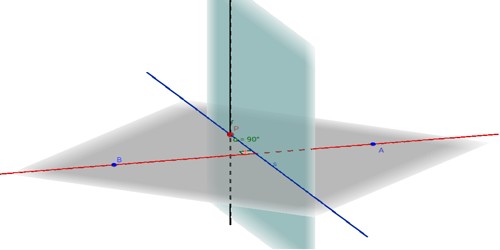
In the adjoining figure, XOX’ and YOY’ are two intersecting and mutually perpendicular straight lines. Together, the two lines form the frame of reference in the Cartesian x-y plane for which
(i) XOX’ is called the x-axis.
(ii) YOY’ is called the y-axis, and
(iii) O is called the origin.
The x-axis and the y-axis divide the x-y plane into four parts, called quadrants, as shown in the figure.
A is the point in the first quadrant whose distance from the y-axis and x-axis are 3 and 4 units respectively. So, the coordinates of A are (3, 4). We express it by writing A = (3, 4). B, C and D are also points whose distance from the y-axis and the x-axis are same as those of point A. But due to their positions in different quadrants, their coordinates are different. Thus, the coordinates of B, in the second quadrant, are (-3, 4); those of C, in the third quadrant, are (-3, -4) and those of D, in the fourth quadrant, are (3, -4)
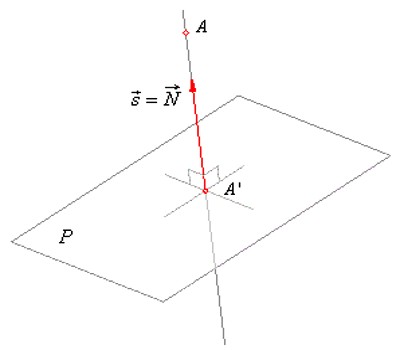
Projection of a point onto a plane
A given point A(x0, y0, z0) and its projection A’ determine a line of which the direction vector s coincides with the normal vector N of the projection plane P.
As the point A’ lies at the same time on the line AA’ and the plane P. the coordinates of the radius (position) vector of a variable point of the line written in the parametric form
x = x0 + a.t, y = y0 + b.t and z = z0 c.t,
These variable coordinates of a point of the line plugged into the equation of the plane will determine the value of the parameter t such that this point will be, at the same time. on the line and the plane.
Information Source: