Properties of Addition
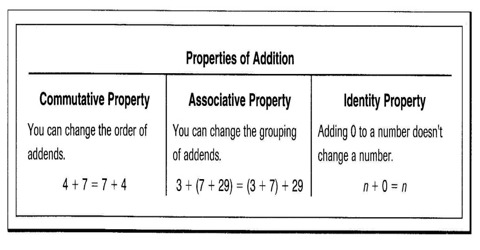
There are four mathematical properties which involve addition. The properties are the commutative, associative, additive identity and distributive properties.
Commutative property: Changing the order of addends does not change the sum.When two numbers are added, the sum is the same regardless of the order of the addends. For example 4 + 2 = 2 + 4
To remember the commutative property, it might be helpful to think about the word commute which means to switch places between home and work (or home and school). In the example above, you can see the 4 and the 2 commuting or switching places.

Associative Property: Changing the grouping of addends does not change the sum. When three or more numbers are added, the sum is the same regardless of the grouping of the addends. For example (2 + 3) + 4 = 2 + (3 + 4)
To remember the associative property, it might be helpful to think about the word associate, which as a verb means to interact with a group (maybe you associate with a certain group of friends!). The parentheses are grouping operators, that is, they form groups of numbers and operations. You can see in the example above, the 3 can associate with either the 2 or the 4, but the value of each side is still a total of 9.
Additive Identity Property: The sum of 0 and any number is that number. The sum of any number and zero is the original number. For example: 5 + 0 = 5.
To remember the identity property, it might be helpful to think of it as a question and answer: What number can I add so that the value is not changed? Zero. In the example above, the 5 gets to keep its identity because adding zero does not change its value.
Distributive property: The sum of two numbers times a third number is equal to the sum of each addend times the third number. For example 4 * (6 + 3) = 4*6 + 4*3
The distributive property is the only property that combines multiplication and addition. That makes it very important!
Information Source: Properties of Addition