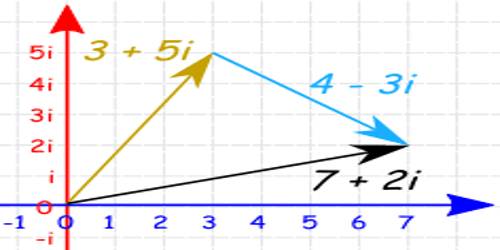
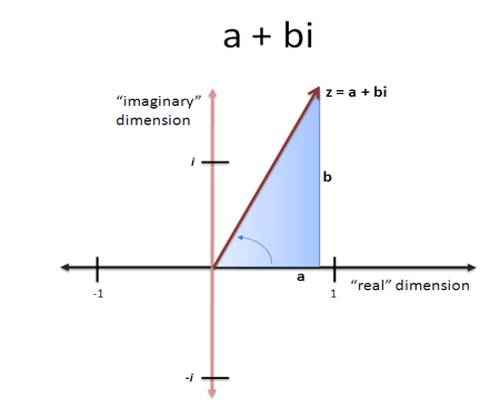
The complex number system can be defined as the algebraic extension of the ordinary real numbers by an imaginary number i. This means that complex numbers can be added, subtracted, and multiplied, as polynomials in the variable i, with the rule i2 = −1 imposed.
A complex number really does keep track of two things at the same time. One of those things is the real part while the other is the imaginary part. For example, z = 3 + 2i is a complex number. The real part of z is 3 and the imaginary part of z is 2.
Properties of Complex Numbers
If x, y are real and x + iy = 0 then x = 0, y = 0.
Proof:
Since, x + iy = 0 = 0 + i0, hence by the definition of equality of two complex numbers it follows that, x = 0 and y = 0.
If x, y, p, q are real and x + iy = p + iq then x = p and y = q.
Proof:
Since x + iy = p + iq
Hence x − p = -i(y − q) ⇒ (x − p)2 = i2 (y − q)2
⇒ (x − p)2 + (y − q)2 = 0 (Since i2 = -1) (1)
Since x, y, p, q are real, (x − p)2 and (y − q)2 are both non-negative. Hence the equation (1) is satisfied if each square is separately zero. Hence,
(x − p)2 = 0 or x = p and (y − q)2 = 0 or y = q.
When a, b are real numbers and a + ib = 0 then a = 0, b = 0
Proof:
According to the property,
a + ib = 0 = 0 + i ∙ 0,
Therefore, from the definition of equality of two complex numbers we conclude that, x = 0 and y = 0.
When a, b, c and d are real numbers and a + ib = c + id then a = c and b = d.
Proof:
According to the property,
a + ib = c + id and a, b, c and d are real numbers.
Therefore, from the definition of equality of two complex numbers, we conclude that; a = c and b = d.
For any three the set complex numbers z11, z22 and z33 satisfies the commutative, associative and distributive laws.
(i) z1 + z2 = z2 + z1 (Commutative law for addition).
(ii) z1 ∙ z1 = z2 ∙ z1 (Commutative law for multiplication).
(iii) (z1 + z2) + z3 = z1 + (z2 + z3) (Associative law for addition)
(iv) (z1z2)z3 = z1(z1z3) (Associative law for multiplication)
(v) z1(z1 + z3) = z1z2 + z1z3 (Distributive law).
Information Source;