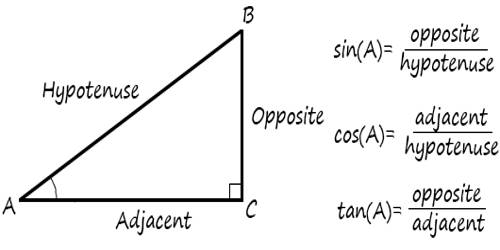
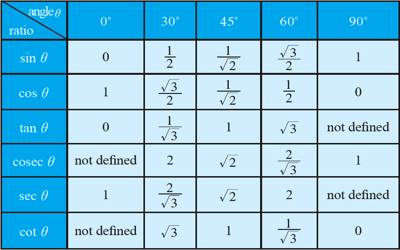
“Trigon” is Greek for the triangle, and “metric” is Greek for measurement. The trigonometric ratios are special measurements of a right triangle (a triangle with one angle measuring 90°). Remember that the two sides of a right triangle which form the right angle are called the legs, and the third side (opposite the right angle) is called the hypotenuse.
- The sine of the angle is the ratio of the length of the side opposite the angle divided by the length of the hypotenuse. It is the trigonometric function that is equal to the ratio of the side opposite a given angle (in a right-angled triangle) to the hypotenuse.
- The cosine of the angle is the ratio of the length of the side adjacent to the angle divided by the length of the hypotenuse. It is the trigonometric function that is equal to the ratio of the side adjacent to an acute angle (in a right-angled triangle) to the hypotenuse.
- The tangent of the angle is the ratio of the length of the side opposite the angle divided by the length of the side adjacent to the angle.
Proving Trigonometric Ratios
In proving trigonometric ratios we will learn how to proof the questions step-by-step using trigonometric identities.
- If sin4x + sin2 x = 1 then proof that, cot4x + cot2 x = 1.
Solution:
Given, sin4x + sin2 x = 1
⇒ sin4x + sin2 x – sin2 x = 1 – sin2 x, [subtract sin2 x from both the sides]
⇒ sin4x = 1 – sin2 x
⇒ sin4x = cos2 x.
Now L.H.S. = cot4x + cot2 x
= cos4x/sin4x + cos2 x/sin2 x
= cos4x/cos2 x + sin4x/sin2 x, [since, sin4x = cos2 x and cos2 x = sin4x]
= 1 = R.H.S. [since we know, sin2 x + cos2 x = 1]
(Proved)
- If sin θ – cos θ = √2 cos θ then proof that sin θ + cos θ = √2 sin θ, where 0 < θ < π/2
Solution:
Given, sin θ – cos θ = √2 cos θ
⇒ (sin θ – cos θ)2 = (√2 cos θ)2, [squaring both the sides]
⇒ sin2 θ + cos2 θ – 2 sin θ cos θ = 2 cos2 θ
⇒ sin2 θ + cos2 θ – 2 sin θ cos θ – cos2 θ = 2 cos2 θ – cos2 θ, [subtract cos2 θ from both the sides]
⇒ sin2 θ – 2 sin θ cos θ = cos2 θ
⇒ sin2 θ – 2 sin θ cos θ + 2 sin θ cos θ = cos2 θ + 2 sin θ cos θ, [adding 2 sin θ cos θ on both the sides]
⇒ sin2 θ = cos2 θ + 2 sin θ cos θ
⇒ sin2 θ + sin2 ϴ = sin2 θ + cos2 θ + 2 sin θ cos θ, [adding sin2 θ on both the sides]
⇒ 2 sin2 θ = (sin θ + cos θ)2
⇒ (sin θ + cos θ)2 = 2 sin2 θ
Now taking square root on both the sides we get,
⇒ sin θ + cos θ = ± √2 sin θ
According to the question, 0 < θ < π/2, hence we neglect the negative vaue.
Therefore, sin θ + cos θ = √2 sin θ
(Proved)
The above explanation on proving trigonometric ratios will help us to solve different types of trigonometric problems.
Information Source: