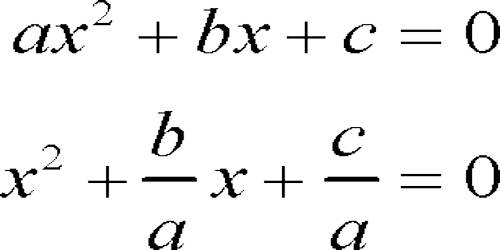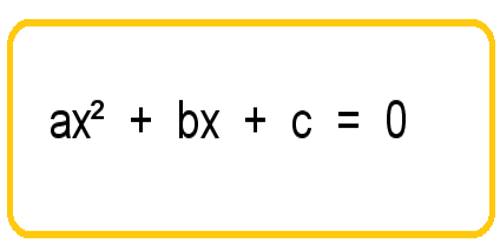A polynomial of the second degree is generally called a quadratic polynomial. In elementary algebra, the quadratic formula is the solution of the quadratic equation. There are other ways to solve the quadratic equation instead of using the quadratic formula, such as factoring, completing the square, or graphing. Using the quadratic formula is often the most convenient way.
If f(x) is a quadratic polynomial, then f(x) = 0 is called a quadratic equation.
An equation in one unknown quantity in the form ax2 + bx + c = 0 is called quadratic equation.
A quadratic equation is an equation of the second degree.
Often, the simplest way to solve “ax2 + bx + c = 0″ for the value of x is to factor the quadratic, set each factor equal to zero, and then solve each factor. But sometimes the quadratic is too messy, or it doesn’t a factor at all, or you just don’t feel like factoring. While factoring may not always be successful, the Quadratic Formula can always find the solution.
The general form of a quadratic equation is ax2 + bx + c = 0 where a, b, c are real numbers (constants) and a ≠ 0, while b and c may be zero.
Here, x is the variable, a is called the coefficient of x2, b the coefficient of x and c the constant (or absolute) term.
The values of x which satisfy the equation are called the roots of the quadratic equation.
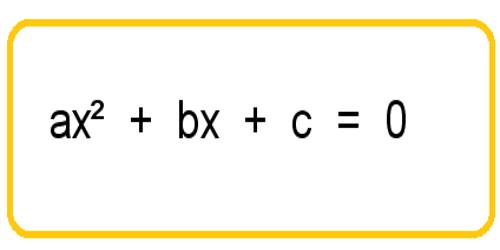
Examples of quadratic equation:
(i) 5x2 + 3x + 2 = 0 is an quadratic equation.
Here, a = the coefficient of x2 = 5,
b = coefficient of x = 3 and
c = constant = 2
(ii) 2m2 – 5 = 0 is an quadratic equation.
Here, a = the coefficient of m2 = 2,
b = coefficient of m = 0 and
c = constant = -5
(iii) (x – 2)(x – 1) = 0 is an quadratic equation.
(x – 2)(x – 1) = 0
⇒ x2 – 3x + 2 = 0
Here, a = the coefficient of x2 = 1,
b = coefficient of x = -3 and
c = constant = 2
(iv) x2 = 1 is an quadratic equation.
x2 = 1
⇒ x2 – 1 = 0
Here, a = the coefficient of x2 = 1,
b = coefficient of x = 0 and
c = constant = -1
(v) p2 – 4p + 4 = 0 is an quadratic equation.
Here, a = the coefficient of p2 = 1,
b = coefficient of p = -4 and
c = constant = 4.
Information Source: