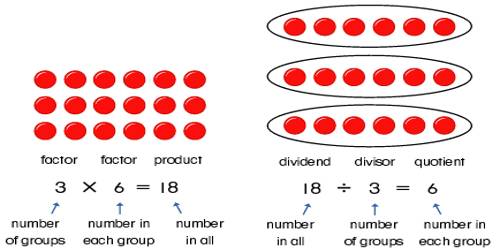
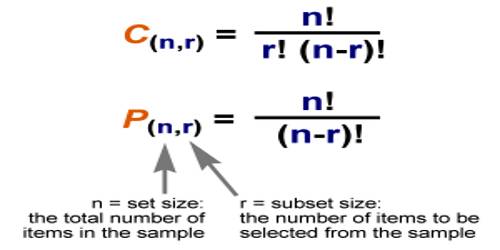
Rational Numbers can be written as a ratio of one number to another. The name rational is based on the word ‘ratio.’ A ratio is a comparison of two or more numbers and is often written as a fraction. A number is considered a rational number if it can be written as one integer divided by another integer. Sometimes this is referred to as a simple fraction. A Rational Number is a real number that can be written as a simple fraction (i.e. as a ratio). Most numbers we use in everyday life are Rational Numbers.
The ancient greek mathematician Pythagoras believed that all numbers were rational, but one of his students Hippasus proved (using geometry, it is thought) that you could not write the square root of 2 as a fraction, and so it was irrational.
A rational number is a number that can be expressed as a fraction p/q where p and q are integers and q ≠ 0. A rational number p/q is said to have numerator p and denominator q. Numbers that are not rational are called irrational numbers. The real line consists of the union of the rational and irrational numbers. The set of rational numbers is of measure zero on the real line, so it is “small” compared to the irrationals and the continuum.

Examples of rational numbers include -7, 0, 1, 1/2, 22/7, 12345/67, and so on. Farey sequences provide a way of systematically enumerating all rational numbers.
The set of rational numbers –
- Involve positive and negative numbers, and zero.
- Can be expressed as a fraction.
The name rational lies on the word ‘ratio’ which is a comparison of two or more values and generally said as a fraction. A number is said to be a rational number if you can write it as one integer divided by the other integer.
Examples of Rational Numbers: each of the numbers 2/3, 5/8, -3/14, -11/-5, 7/-9, 7/-15 and -6/-11 is a rational number.
- 5; You can express 5 as 5/1 which is the quotient of the integer 5 and 1
- 2; You can express 2 as 2/1 which is the quotient of the integer 2 and 1
- √9; is rational because you can simplify the square root to 3 which is the quotient of the integer 3 and 1
- 5; is rational because it can be expressed as 3/2
Information Source: