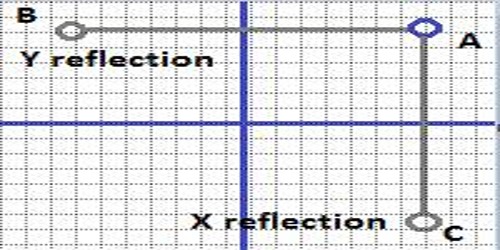
Reflection of Point in Y-Axis
A reflection can be thought of as folding or “flipping” an object over the line of reflection. An object and its reflection have the same shape and size, but the figures face in opposite directions. The objects appear as if they are mirror reflections, with right and left reversed.
When you reflect a point across the y-axis, the y-coordinate remains the same, but the x-coordinate is transformed into its opposite (its sign is changed).
Reflection in the line x = 0 i.e., in the y-axis.
The line x = 0 means the y-axis.
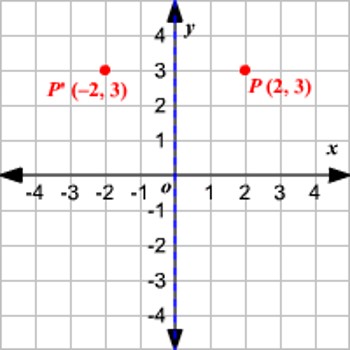
Let P be a point whose coordinates are (x, y).
Let the image of P be P’ in the y-axis.
Clearly, P’ will be similarly situated on that side of OY which is opposite to P. So, the x-coordinates of P’ will be – x while its y-coordinates will remain same as that of P.
The image of the point (x, y) in the y-axis is the point (-x, y).
Symbolically, My (x, y) = (-x, y)
Rules to find the reflection of a point in y-axis:
- Change the sign of abscissa i.e. x-coordinate.
- Retain the ordinate i.e., y-coordinate.
Therefore, when a point is reflected in the y-axis, the sign of its abscissa changes.
Examples:
(i) The image of the point (3, 4) in the y-axis is the point (-3, 4).
(ii) The image of the point (-3, -4) in the y-axis is the point (-(-3), -4) i.e., (3, -4).
(iii) The image of the point (0, 7) in the y-axis is the point (0, 7).
(iv) The image of the point (-6, 5) in the y-axis is the point (-(-6), 5) i.e., (6, 5).
(v) The reflection of the point (5, 0) in the y-axis = (-5, 0) i.e., My (5, 0) = (-5, 0)
Solved example to find the reflection of a point in the y-axis:
Find the points onto which the points (11, -8), (-6, -2) and (0, 4) are mapped when reflected in the y-axis.
Solution:
We know that a point (x, y) maps onto (-x, y) when reflected in the y-axis. So, (11, -8) maps onto (-11, -8); (-6, -2) maps onto (6, -2) and (0, 4) maps onto (0, 4).
Information Source: