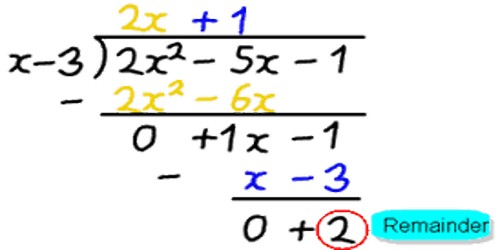Remainder Theorem

Remainder Theorem:

The Remainder Theorem is a useful mathematical theorem that can be used to factorize polynomials of any degree in a neat and fast manner. It is useful for evaluating polynomials at a given value of x, though it might not seem so, at least at first blush.

The Remainder Theorem states that when you divide a polynomial P(x) by any factor (x – a); which is not necessarily a factor of the polynomial; you’ll obtain a new smaller polynomial and a remainder, and this remainder is the value of P(x) at x = a, i.e P(a)

Let p(x) be any polynomial of degree greater than or equal to 1 and let α be any real number. If p(x) is divided by the polynomial (x – α), then the remainder is p(α).

In other words:

If the polynomial f(x) is divided by x – α then the remainder R is given by f(x) = (x – α) q(x) + R, where q(x) is the quotient and R is a constant (because the degree of the remainder is less than the degree of the divisor x – α).

Putting x = α, f(α) = (α – α)q(α) + R or f(α) = R

When the polynomial f(x) is divided by x – α, the remainder R = f(α) = value of f(x) when x is α.

Remainder Theorem operates on the fact that a polynomial is completely divisible once by its factor to obtain a smaller polynomial and a remainder of zero. This provides an easy way to test whether a value a is a root of the polynomial P(x).

For example, given a polynomial P(x), and also given that a is a root of the polynomial, then when P(x) is divided by the factor (x – a), the result should be a smaller polynomial P1(x) and a remainder zero.

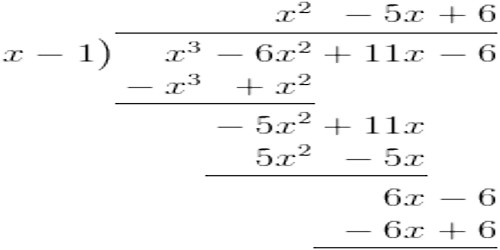
Explanation

If you divide a polynomial f(x) by (x – h), then the remainder is f(h).

The theorem states that our remainder equals f(h). Therefore, we do not need to use long division, but just need to evaluate the polynomial when x = h to find the remainder.

We should understand why this theorem is true. Why does this work?

Let’s set up our division problem using the notation in the theorem. If we divide some polynomial f(x) with a divisor in the form of (x – h) of which h is a real number, then we will get a quotient, which we will call p(x), and a remainder, which we will call r. Our division problem will look as follows:

f(x)/(x – h) = p(x) with a remainder of r

Like we did with our simple division problems in integers, we can manipulate this function to get the following.

f(x) = (x – h) * p(x) + r

Let’s say we want to evaluate our polynomial at x = h. Therefore, (x – h) = (h – h) = 0. Let’s look at the following statements. Statement 1 shows our equation. In statement 2, we substitute h for x. Then we simplify in statements 3 and 4.