Replacement Set and Solution Set in Set Notation
Replacement Set: It is a set of elements any one of which may be used to replace a given variable or placeholder in a mathematical sentence or expression (such as an equation). The set, from which the values of the variable which involved in the inequation, are chosen, is known as replacement set.
Solution Set: In mathematics, a solution set is the set of values that satisfy a given set of equations or inequalities. A solution to an inequation is a number chosen from the replacement set which, satisfy the given inequation. The set of all solutions of an inequation is known as solution set of the inequation.
For example:
Let the given inequation be y < 6, if:
(i) The replacement set = N, the set of natural numbers;
The solution set = {1, 2, 3, 4, 5}.
(ii) The replacement set = W, the set of whole numbers;
The Solution set = {0, 2, 3, 4, 5}.
(iii) The replacement set = Z or I, the set of integers;
The solution set = {………, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5}
But, if the replacement set is the set of real numbers, the solution set can only be described in set-buider form, i.e., {x : x ∈ R and y < 6}.
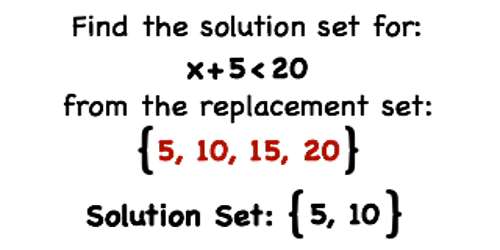
Example on replacement set and solution set in set notation:
If the replacement set is the set of whole numbers (W), find the solution set of 4z – 2 < 2z + 10.
Solution:
4z – 2 < 2z + 10
⟹ 4z – 2 + 2< 2z + 10 + 2, [Adding 2 on both the sides]
⟹ 4z < 2z + 12
⟹ 4z – 2z < 2z + 12 – 2z, [Subtracting 2z from both sides]
⟹2z < 12
⟹ 2z/2 <12/2 [Dividing both sides by 2]
⟹ z < 6
Since the replacement set = W (whole numbers)
Therefore, the solution set = {0, 1, 2, 3, 4, 5}
A solution is any value of a variable that makes the specified equation true. A solution set is the set of all variables that makes the equation true. The solution set of 2y + 6 = 14 is {4} , because 2(4) + 6 = 14 . The solution set of y 2 + 6 = 5y is {2, 3} because 22 + 6 = 5(2) and 32 + 6 = 5(3) . If an equation has no solutions, its solution set is the empty set or null set–a set with no members, denoted Ø . For example, the solution set to x 2 = – 9 is Ø, because no number, when squared, is equal to a negative number.
Information Source: