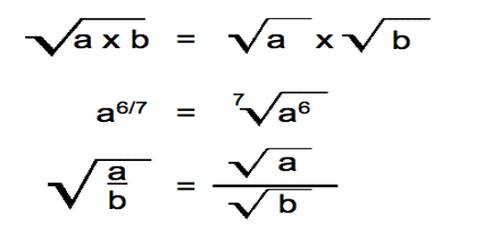Surds are numbers left in root form (√) to express its exact value. It has an infinite number of non-recurring decimals. Therefore, surds are irrational numbers. There are certain rules that we follow to simplify an expression involving surds.
A root of a positive real quantity is called a surd if its value cannot be exactly determined. It is a number that can’t be simplified to remove a square root (or cube root etc). For example, each of the quantities √3, ∛7, ∜19, (16)^2/5 etc. is a surd.
More Examples:
- √2 (square root of 2) can’t be simplified further so it is a surd
- √4 (square root of 4) CAN be simplified to 2, so it is NOT a surd
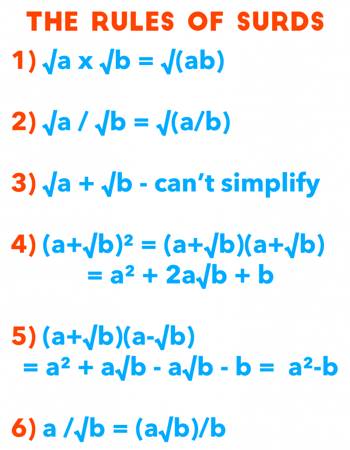
Rules of Surds
Some of the important rules of surds are listed below.
- Every rational number is not a surd.
- Every irrational number is a surd.
- A root of a positive real quantity is called a surd if its value cannot he exactly determined.
√9, ∛64, ∜(16/81) etc. are rational numbers but not surds because √9 = 3, ∛64 = 4, ∜(16/81) = 2/3 etc.
- √a × √a = a ⇒ √5 × √5 = 5
- The sum and difference of two simple quadratic surds are said to be conjugate surds or complementary surds to each other. Thus, (4√7 + √6) and (4√7 – √6) are surds conjugate to each other.
- To express in the simplest form, denominator must be rationalized.
- The method of convening a given surd into a rational number on multiplication by another suitable surd is called rationalization of surds. In this case the multiplying surd is called the rationalizing factor of the given surd and conversely.
- If a and b are both rationals and √x and √y are both surds and a + √x = b + √y then a = b and x = y
- If a – √x = b – √y then a = b and x = y.
- If a + √x = 0, then a = 0 and x = 0.
- If a – √x = 0, then a = 0 and x = 0.
Information Source;