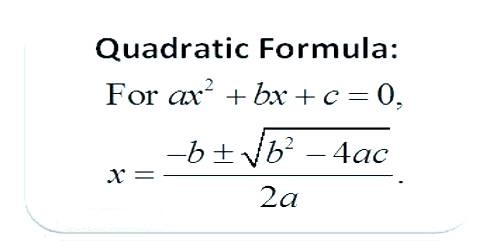A polynomial of the second degree is generally called a quadratic polynomial. In elementary algebra, the quadratic formula is the solution of the quadratic equation. There are other ways to solve the quadratic equation instead of using the quadratic formula, such as factoring, completing the square, or graphing. Using the quadratic formula is often the most convenient way.
If f(x) is a quadratic polynomial, then f(x) = 0 is called a quadratic equation.
An equation in one unknown quantity in the form ax2 + bx + c = 0 is called quadratic equation.
Sign of the Quadratic Expression
We already acquainted with the general form of quadratic expression ax2 + bx + c now, here discuss the sign of the quadratic expression ax2 + bx + c = 0 (a ≠ 0).
When x be real then, the sign of the quadratic expression ax2 + bx + c is the same as a, except when the roots of the quadratic equation ax2 + bx + c = 0 (a ≠ 0) are real and unequal and x lies between them.
Proof:
We know the general form of quadratic equation ax2 + bx + c = 0 (a ≠ 0) ………………… (i)
Let α and β be the roots of the equation ax2 + bx + c = 0 (a ≠ 0). Then, we get
α + β = -b/a and αβ = c/a
Now, ax2 + bx + c = a(x2 + b/a x + c/a)
= a[x2 – (α + β)x + αβ]
= a[x(x – α) – β(x – α)]
or, ax2 + bx + c = a(x – α)(x – β) ………………… (ii)
Case I:
Let us assume that the roots α and β of equation ax2 + bx + c = 0 (a ≠ 0) are real and unequal and α > β. If x be real and β < x < α then,
x – α < 0 and x – β > 0
Therefore, (x – α)(x – β) < 0
Therefore, from ax2 + bx + c = a(x – α)(x – β) we get,
ax2 + bx + c > 0 when a < 0
and ax2 + bx + c < 0 when a > 0
Therefore, the quadratic expression ax2 + bx + c has a sign of opposite to that of a when the roots of ax2 + bx + c = 0 (a ≠ 0) are real and unequal and x lie between them.

Case II:
Let the roots of the equation ax2 + bx + c = 0 (a ≠ 0) be real and equal i.e., α = β.
Then, from ax2 + bx + c = a(x – α)(x – β) we have,
ax2 + bx + c = a(x – α)2 ……………. (iii)
Now, for real values of x we have, (x – α)2 > 0.
Therefore, from ax2 + bx + c = a(x – α)2 we clearly see that the quadratic expression ax2 + bx + c has the same sign as a.
Case III:
Let us assume α and β be real and unequal and α > β. If x is real and x < β then,
x – α < 0 (Since, x < β and β < α) and x – β < 0
(x – α)(x – β) > 0
Now, if x > α then x – α >0 and x – β > 0 ( Since, β < α)
(x – α)(x – β) > 0
Therefore, if x < β or x > α then from ax2 + bx + c = a(x – α)(x – β) we get,
ax2 + bx + c > 0 when a > 0
and ax2 + bx + c < 0 when a < 0
Therefore, the quadratic expression ax2 + bx + c has the same sign as a when the roots of the equation ax2 + bx + c = 0 (a ≠ 0) are real and unequal and x does not lie between them.
Notes:
(i) When the discriminant b2 – 4ac = 0 then the roots of the quadratic equation ax2 + bx + c = 0 are equal. Therefore, for all real x, the quadratic expression ax2 + bx + c becomes a perfect square when discriminant b2 -4ac = 0.
(ii) When a, b are c are rational and discriminant b2 – 4ac is a positive perfect square the quadratic expression ax2 + bx + c can be expressed as the product of two linear factors with rational coefficients.
Information Source: