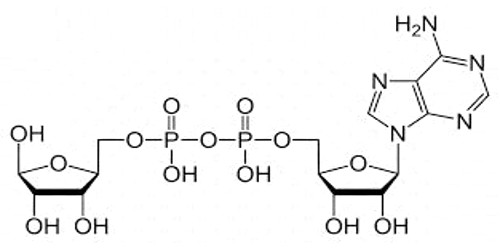
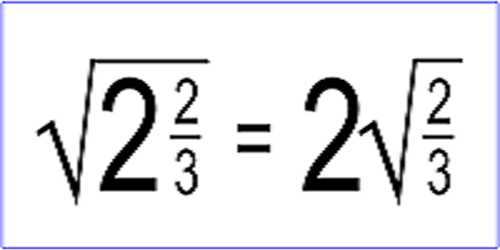Simple and Compound Surds
Surds are numbers left in root form (√) to express its exact value. It has an infinite number of non-recurring decimals. Therefore, surds are irrational numbers. A root of a positive real quantity is called a surd if its value cannot be exactly determined. It is a number that can’t be simplified to remove a square root (or cube root etc). For example, each of the quantities √3, ∛7, ∜19, (16)^2/5 etc. is a surd.
More Examples:
- √2 (square root of 2) can’t be simplified further so it is a surd
- √4 (square root of 4) can be simplified to 2, so it is NOT a surd
From the definition, it is evident that a surd is an incommensurable quantity, although its value can be determined to any degree of accuracy.
Simple Surds are such as are expressed by one single term; as √2, or √3a, & c.
Compound Surds, are such as consist of two or more simple Surds connected together by the signs + or -; as √3 + √2, or √3 – √2, or √3(5 + √2): which last is called a universal root, and denotes the cubic root of the sum arising by adding 5 and the root of 2 together.
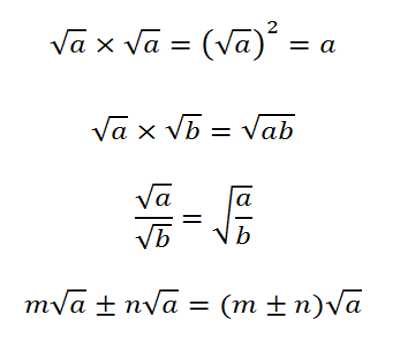
Definition of Simple Surd:
A surd having a single term only is called a monomial or simple surd.
For example, each of the surds √2, ∛7, ∜6, 7√3, 2√a, 5∛3, m∛n, 5∙73/5 etc. is a simple surd.
Definition of Compound Surd:
The algebraic sum of two or more simple surds or the algebraic sum of a rational number and simple surds is called a compound scud. Compound surds are sum or difference of two other surds.
For example, each of the surds (√5 + √7), (√5 – √7), (5√8 – ∛7), (∜6 + 9), (∛7 + ∜6), (x∛y – b) is a compound surd.
Note: The compound surd is also known as binomial surd. That is, the algebraic sum of two surds or a surd and a rational number is called a binomial surd.
For example, each of the surds (√5 + 2), (5 – ∜6), (√2 + ∛7) etc. is a binomial surd.
Information Source: