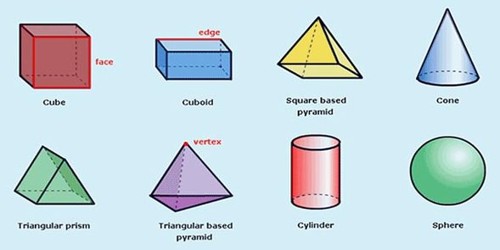
In mathematics, solid geometry is the traditional name for the geometry of three-dimensional Euclidean space. Examples like cones, cylinders, prisms, pyramids, polyhedra, and spheres. Solid geometry also includes the study of points, lines, shapes, and regions in relation to solids and surfaces.
Solids have properties (special things about them), such as:
- volume (think of how much water it could hold)
- surface area (think of the area you would have to paint)
- how many vertices (corner points), faces and edges they have
Solid geometry terms:
(i) Dimension: Each of length, breadth, and thickness of anybody is called a dimension of the body.
(ii) Point: A point has no dimension, that is, it has neither length nor breadth nor thickness; it has position only.
(iii) Line: A line has length only but no breadth and thickness. Therefore, a line has one dimension, that is, it is one dimensional.
(iv) Surface: A surface has length and breadth but no thickness. Therefore, a surface has two dimensions, that is, it is two dimensional.
(v) Solid: A solid has length, breadth, and thickness. Therefore, a solid has three dimensions, that is, it is three dimensional.
The book is a solid, each of its six faces is a surface, each of its edges is a line and each of its corners is a point.
A line is bounded by points, a surface is bounded by lines and a solid is bounded by surfaces. In other words, a line is generated by the motion of a point, a surface is generated by the motion of a line and a solid is generated by the motion of a surface.
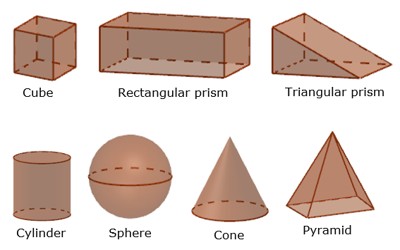
(vi) Solid Geometry: The branch of geometry which deals with the properties of points, lines, surfaces and solids in three-dimensional space is called solid geometry.
(vii) Plane or Plane Surface: If the straight line joining two points on a surface lies wholly on the surface then the surface is called a plane surface or a plane.
A straight line may be extended indefinitely in either direction, that is, straight lines are supposed to be of infinite length. Similarly, planes are also assumed to be of infinite extent, unless otherwise stated. The statement that a straight line lies wholly on a surface signifies that every point on the line (however produced in both directions) lies on the surface.
Information Source: