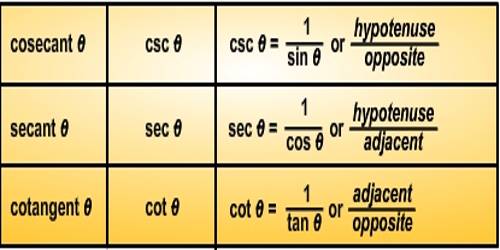
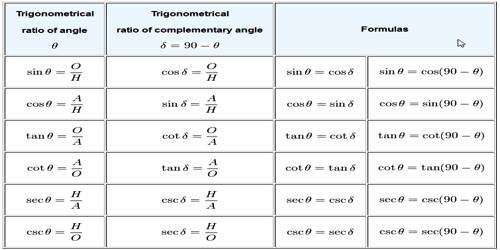
Have you ever encountered a math issue so complex that you had to design a new number type? Quadratic equations, as you may (or may not, depending on your age) recall from high school, are a type of equation. They appear as follows:
ax^2+bx+c=0
If you recall a few tricks, they are not too tough to solve. Let us pretend we have a quadratic equation.
x^2+5x+6=0
In addition, we are trying to find out what x stands for. There are several techniques to solve this algebraic problem nowadays, but they all provide the same result:
x=-2 or -3
It was, however, a different story 500 years ago. To begin with, it would not have been an algebraic issue with an equation — it would have been geometry.
The approach employed by medieval mathematicians is known as “completing the square” in modern parlance. It is rather good, and it gets the job done well. Is it, however, applicable to larger, nastier equations? We do not want to solve a quadratic equation and instead tackle a dense problem.
ax^3+bx^2+cx+d=0
Mathematicians had been perplexed by cubic equations for ages, even as early as the 1500s. Clearly, they could solve (at least in some cases): simply look at the equation.
x^3+2x^2-5x-6=0
If we change the left-hand side to x = 2, we get,
2^3+2*2^2-5*2-6=8+8-10-6=0
So, yes, x = 2 is a solution — but are there any others? In addition, how are we going to locate them without relying on guesswork?
It is feasible, as Veritasium demonstrates, although medieval mathematicians did not think so. That is because solving a cubic equation occasionally (or perhaps frequently) forces us to step outside of the domain of real numbers. As we have already established, a real number is the type of number that comes to mind when you are told to “think of a number.” So seven two the recurrent negative 14.2 and pi are all actual numbers. We often see them as represented by a number line, such as this.
Real numbers have many cool qualities, but one of them is that they are not “algebraically closed,” as mathematicians describe it. That is, you can apply some type of algebra — timesing, dividing, squaring, or anything similar – that allows you to start with a real number and end with something else. What exactly is this algebra? It is as simple as taking the square root of a number, taking the square root of a negative integer, in particular.
We taught that the square root of a negative integer “doesn’t exist and ye olde mathematicians believed the same thing — when these roots appeared in cubic equations, the problems simply labeled “impossible,” and the solver moved on. However, in 1572, an engineer named Rafael Bombelli achieved a breakthrough by f*cking about and finding out, as only an engineer can. He reasoned, we just assume that square roots of negative numbers are not a problem. What happens if we leave them in and solve the problem without them? Do we get a response? What is more essential, do we obtain the correct answer?
His bet paid off: it was successful. Bombelli not only figured out how to solve cubic equations, but he also came up with the concept of imaginary numbers. These imaginary numbers – whose term originally meant as a slur by Rene Descartes, who despised them – went on to revolutionize mathematics and the world, as we know it. According to Veritasium, it allowed scientists to very separate algebra from geometry, allowing for discoveries in domains like electrical engineering and fluid dynamics. It even appears in sciences like relativity and quantum physics, which would have been unthinkable to the renaissance mathematicians who first conceived of them.
“Schrödinger inserted the square root of minus one into the equation, and suddenly everything made sense,” famed scientist Freeman Dyson, cited in the movie, said. Everything we know about atom behavior is accurately described by the Schrödinger equation.
It is the foundation of all chemistry and the majority of physics. And that minus one square root indicates that nature operates with complex numbers rather than actual numbers.”