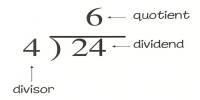Trigonometric Angles
The word ‘Trigonometry’ has been derived from Greek words ‘trigon’ meaning three angles and ‘metron’ which means measurement. The angles mπ/n (with m, n integers) for which the trigonometric functions may be expressed in terms of finite root extraction of real numbers are limited to values of m which are precisely those which produce constructible polygons.
Therefore, basically, the object of trigonometry was to deal with the measurement of triangles. Trigonometry was also involved in the establishment of relations between the sides, angles, and area of a triangle. Nowadays, the object of trigonometry deals not only with the angles of a triangle but the measure of all sorts of positive and negative angles. Thus this branch of mathematics has widened. Trigonometry is also used in science which involves measurement of angles.
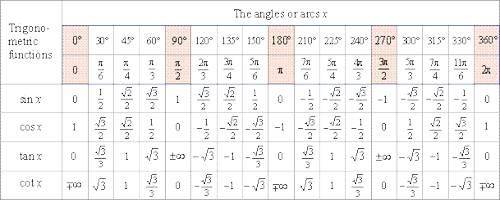
Important to know about Trigonometric angles:
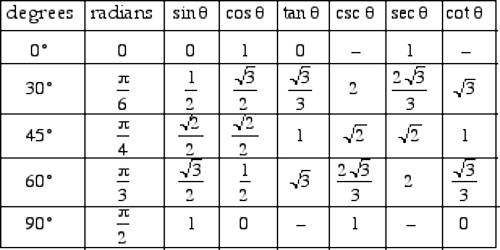
Radian: In circular measure, a radian is the unit of angle. It is defined as the angle subtended at the center of a circle by an arc whose length is equal to the radius of the circle.
A radian is a constant angle.
1 radian = 2/π right angle = 57°17′ (44.8)” (approx.)
90°= 100g = πc/2; πc = 180.
If the sexagesimal, centesimal and circular measures of a given angle be D°, Gg and Rc respectively then,
D/180 = G/200 = R/π.
If r is the radius of a circle then its circumference = 2πr where π is a constant whose approximate value is 22/7 and more accurate value is 3.14159.
Generally, the unit radian is not mentioned in the measurement of an angle in the circular system. For example, the angle πc/2 is usually written as π/2.Therefore, if the unit in the measurement of an angle is not mentioned, it is to be taken in circular unit i.e., in radian. Thus, an angle having measure 2 means 2c, π/6 means πc/6; note that, an angle π/4 means πc/4 = 180°/4 = 45°.
If an arc of length s of a circle of radius r subtends an angle θ radian at its center then
s = rθ
or, θ = s/r.
Information Source: