Trigonometrical identity
An equation which is true for all values of the variable involved is called an identity. An equation which involves trigonometric ratios of an angle and is true for all the values of the angle is called trigonometrical identities. Trigonometric identities are equations involving the trigonometric functions that are true for every value of the variables involved.
When the solutions of any trigonometric ratio problems represent the same expression in the L.H.S. and R.H.S. and the relation is satisfied for all the values of θ then such relation is called a trigonometrical identity.
A trigonomitric identity is a statement involving trigonometric functions which is true for all possible values of the variables involved. Mutual relations among the trigonometrical ratios are generally used to establish the equality of such trigonometrical identities.
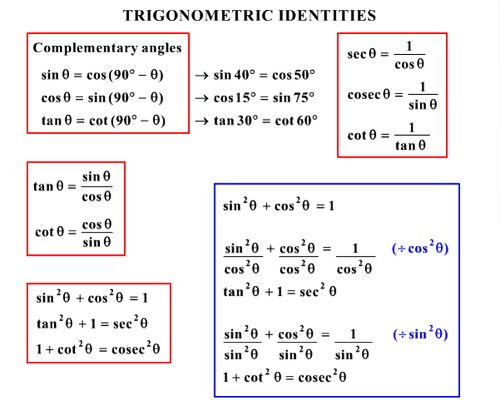
To solve different types of trignometrical identity follow the formula:
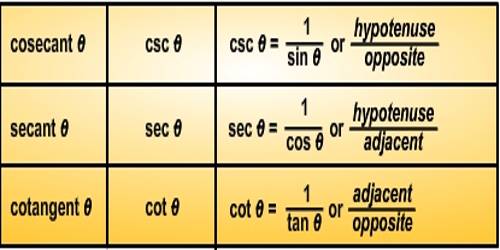
- sin θ ∙ csc θ = 1 ⇒ csc θ = 1/sin θ
- cos θ ∙ sec θ = 1 ⇒ sec θ = 1/cos θ
- tan θ ∙ cot θ = 1 ⇒ cot θ = 1/tan θ
- tan θ = sin θ/cos θ
- cot θ = cos θ/sin θ
- sin2 θ implies (sin θ)2
Similarly, tan3 θ means (tan θ)3 etc.
- sin2 θ + cos2 θ = 1
cos2 θ = 1 – sin2 θ
sin2 θ = 1 – cos2 θ
- sec2 θ = 1 + tan2 θ
sec2 θ – tan2 θ = 1
tan2 θ = sec2 θ – 1
- sec2 θ = 1 + cot2 θ
sec2 θ – 1 = cot2 θ
sec2 θ – cot2 θ = 1
The trigonometrical ratios of a positive acute angle θ are always non-negative and
(i) sin θ and cos θ can never be greater than 1;
(ii) sec θ and csc θ can never be less than 1;
(iii) tan θ and cot θ can have any value.
Information Source: